
如圖1,在Rt△ABC中,∠C=90°,BC=8厘米,點(diǎn)D在AC上,CD=3厘米.點(diǎn)P、Q分別由A、C兩點(diǎn)同時出發(fā),點(diǎn)P沿AC方向向點(diǎn)C勻速移動,速度為每秒k厘米,行完AC全程用時8秒;點(diǎn)Q沿CB方向向點(diǎn)B勻速移動,速度為每秒1厘米.設(shè)運(yùn)動的時間為x秒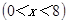 ,△DCQ的面積為y1平方厘米,△PCQ的面積為y2平方厘米.
,△DCQ的面積為y1平方厘米,△PCQ的面積為y2平方厘米.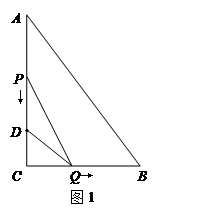
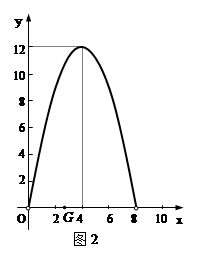
(1)求y1與x的函數(shù)關(guān)系,并在圖2中畫出y1的圖象;
(2)如圖2,y2的圖象是拋物線的一部分,其頂點(diǎn)坐標(biāo)是(4,12),求點(diǎn)P的速度及AC的長;
(3)在圖2中,點(diǎn)G是x軸正半軸上一點(diǎn)(0<OG<6),過G作EF垂直于x軸,分別交y1、y2于點(diǎn)E、F.
①說出線段EF的長在圖1中所表示的實(shí)際意義;
②當(dāng)0<x<6時,求線段EF長的最大值.
(1)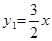 .圖象如圖所示:
.圖象如圖所示: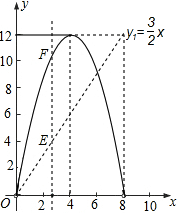
(2)點(diǎn)P的速度每秒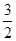 厘米,AC=12厘米;
厘米,AC=12厘米;
(3)①表示△PCQ與△DCQ的面積差(或△PDQ面積);②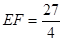
解析試題分析:(1)已知了CD=3,根據(jù)Q點(diǎn)的速度可以用時間x表示出CQ的長,可根據(jù)三角形的面積計算公式得出y1,x的函數(shù)關(guān)系式;
(2)可先求出y2的函數(shù)式,然后根據(jù)其頂點(diǎn)坐標(biāo)來確定k的取值.已知了P點(diǎn)走完AC用時8s,因此AC=8k,而AP=kx,CQ=x,那么可根據(jù)三角形的面積公式列出關(guān)于y2,x的函數(shù)關(guān)系式,進(jìn)而可根據(jù)頂點(diǎn)坐標(biāo)求出k的值;
(3)EF其實(shí)就是y2-y1,也就是三角形PCQ和CDQ的面積差即三角形PDQ的面積.得出EF的函數(shù)關(guān)系式后,根據(jù)自變量的取值以及函數(shù)的性質(zhì)即可求出EF的最大值.
(1)∵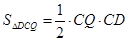 ,CD=3,CQ=x,
,CD=3,CQ=x,
∴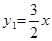 .圖象如圖所示:
.圖象如圖所示:
(2) ,CP=8k-xk,CQ=x,
,CP=8k-xk,CQ=x,
∴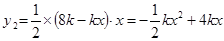 .
.
∵拋物線頂點(diǎn)坐標(biāo)是(4,12),
∴ .解得
.解得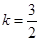
則點(diǎn)P的速度每秒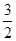 厘米,AC=12厘米;
厘米,AC=12厘米;
(3)①觀察圖象,知線段的長EF=y(tǒng)2-y1,表示△PCQ與△DCQ的面積差(或△PDQ面積)
②由(2)得 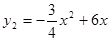 .
.
∵EF=y(tǒng)2-y1,
∴EF=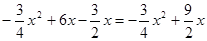 ,
,
∵二次項(xiàng)系數(shù)小于0,
∴在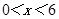 范圍,當(dāng)
范圍,當(dāng)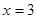 時,
時,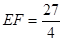 最大.
最大.
考點(diǎn):二次函數(shù)的綜合題
點(diǎn)評:本題知識點(diǎn)多,綜合性強(qiáng),難度較大,一般是中考壓軸題,主要考查學(xué)生對二次函數(shù)的熟練掌握情況.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
| 2 |

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| OC2 |
| 1 |
| OD2 |
| 1 |
| OM2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com