
已知拋物線y=ax2+bx+c(a≠0)的頂點坐標(biāo)為(4,﹣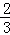 ),且與y軸交于點C(0,2),與x軸交于A,B兩點(點A在點B的左邊).
),且與y軸交于點C(0,2),與x軸交于A,B兩點(點A在點B的左邊).
(1)求拋物線的解析式及A,B兩點的坐標(biāo);
(2)在(1)中拋物線的對稱軸l上是否存在一點P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,請說明理由;
(1)拋物線的解析式為:y= x2﹣
x2﹣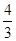 x+2 ,A(2,0),B(6,0);
x+2 ,A(2,0),B(6,0);
(2)存在一點P,使AP+CP的值最小,AP+CP的最小值為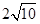 .
.
解析試題分析:(1)根據(jù)知拋物線的頂點坐標(biāo),設(shè)拋物線的解析式為y=a(x﹣4)2﹣ ,再根據(jù)拋物線經(jīng)過(0,2)求出拋物線解析式,進(jìn)而求出A,B兩點的坐標(biāo);
,再根據(jù)拋物線經(jīng)過(0,2)求出拋物線解析式,進(jìn)而求出A,B兩點的坐標(biāo);
(2)線段BC的長即為AP+CP的最小值.
試題解析:(1)由題意,設(shè)拋物線的解析式為y=a(x﹣4)2﹣ (a≠0)
(a≠0)
∵拋物線經(jīng)過(0,2)
∴a(0﹣4)2﹣ =2
=2
解得:a=
∴y= (x﹣4)2﹣
(x﹣4)2﹣
即拋物線的解析式為:y= x2﹣
x2﹣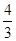 x+2
x+2
當(dāng)y=0時, x2﹣
x2﹣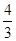 x+2=0
x+2=0
解得:x=2或x=6
∴A(2,0),B(6,0);
(2)存在,
由(1)知:拋物線的對稱軸l為x=4,
因為A、B兩點關(guān)于l對稱,連接CB交l于點P,則AP=BP,
所以AP+CP=BC的值最小
∵B(6,0),C(0,2)
∴OB=6,OC=2
∴BC=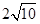 ,
,
∴AP+CP=BC=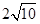
∴AP+CP的最小值為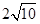 .
.
考點:二次函數(shù)相關(guān).


科目:初中數(shù)學(xué) 來源: 題型:解答題
拋物線頂點坐標(biāo)為點C(1,4),交x軸于點A(3,0),交y軸于點B.
(1)求此拋物線的解析式;
(2)拋物線上是否存在點P,使 ,若存在,求出P點坐標(biāo);若不存在,請說明理由.
,若存在,求出P點坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
動物園計劃用長為120米的鐵絲圍成如圖所示的兔籠,(不包括頂棚)供學(xué)習(xí)小組的同學(xué)參觀,其中一面靠墻,(墻足夠長)怎樣設(shè)計圍成的面積最大?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知直線 分別與y軸、x軸相交于A、B兩點,與二次函數(shù)
分別與y軸、x軸相交于A、B兩點,與二次函數(shù) 的圖像交于A、C兩點.
的圖像交于A、C兩點.
(1)當(dāng)點C坐標(biāo)為( ,
,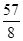 )時,求直線AB的解析式;
)時,求直線AB的解析式;
(2)在(1)中,如圖,將△ABO沿y軸翻折180°,若點B的對應(yīng)點D恰好落在二次函數(shù) 的圖像上,求點D到直線AB的距離;
的圖像上,求點D到直線AB的距離;
(3)當(dāng)-1≤x≤1時,二次函數(shù) 有最小值-3,求實數(shù)m的值.
有最小值-3,求實數(shù)m的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知二次函數(shù) 的圖象經(jīng)過點(4,3),(3,0).
的圖象經(jīng)過點(4,3),(3,0).
(1)求b、c的值;
(2)求出該二次函數(shù)圖象的頂點坐標(biāo)和對稱軸,并在所給坐標(biāo)系中畫出該函數(shù)的圖象;
(3)該函數(shù)的圖像經(jīng)過怎樣的平移得到 的圖像?
的圖像?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知拋物線 (m是常數(shù),
(m是常數(shù),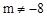 )與x軸有兩個不同的交點A、B,點A、點B關(guān)于直線x=1對稱,拋物線的頂點為C.
)與x軸有兩個不同的交點A、B,點A、點B關(guān)于直線x=1對稱,拋物線的頂點為C.
(1)此拋物線的解析式;
(2)求點A、B、C的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
在平面直角坐標(biāo)系xOy中,拋物線 與x軸交于A、B兩點(點A在點B的左側(cè)),與y軸交于點C(0,4),D為OC的中點.
與x軸交于A、B兩點(點A在點B的左側(cè)),與y軸交于點C(0,4),D為OC的中點.
(1)求m的值;
(2)拋物線的對稱軸與 x軸交于點E,在直線AD上是否存在點F,使得以點A、B、F為頂點的三角形與△ADE 相似?若存在,請求出點F的坐標(biāo),若不存在,請說明理由;
(3)在拋物線的對稱軸上是否存在點G,使△GBC中BC邊上的高為 ?若存在,求出點G的坐標(biāo);若不存在請說明理由.
?若存在,求出點G的坐標(biāo);若不存在請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
二次函數(shù) 的圖象與x軸交于點A(-1, 0),與y軸交于點C(0,-5),且經(jīng)過點D(3,-8).
的圖象與x軸交于點A(-1, 0),與y軸交于點C(0,-5),且經(jīng)過點D(3,-8).
(1)求此二次函數(shù)的解析式和頂點坐標(biāo);
(2)請你寫出一種平移的方法,使平移后拋物線的頂點落在原點處,并寫出平移后拋物線的解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,已知△OAB的頂點A(﹣6,0),B(0,2),O是坐標(biāo)原點,將△OAB繞點O按順時針旋轉(zhuǎn)90°,得到△ODC.
(1)寫出C,D兩點的坐標(biāo);
(2)求過A,D,C三點的拋物線的解析式,并求此拋物線頂點E的坐標(biāo);
(3)證明AB⊥BE.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com