
已知二次函數圖象頂點為C(1,0),直線 與該二次函數交于A,B兩點,其中A點(3,4),B點在y軸上.
與該二次函數交于A,B兩點,其中A點(3,4),B點在y軸上.
(1)求此二次函數的解析式;
(2)P為線段AB上一動點(不與A,B重合),過點P作y軸的平行線與二次函數交于點E.設線段PE長為h,點P橫坐標為x,求h與x之間的函數關系式;
(3)D為線段AB與二次函數對稱軸的交點,在AB上是否存在一點P,使四邊形DCEP為平行四邊形?若存在,請求出P點坐標;若不存在,請說明理由.
(1)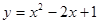 ;(2)
;(2)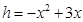 ;(3)存在,P點坐標為(2,3).
;(3)存在,P點坐標為(2,3).
解析試題分析:(1)因為直線y=x+m過點A,將A點坐標直接代入解析式即可求得m的值;設出二次函數的頂點式,將(3,4)代入即可;
(2)由于P和E的橫坐標相同,將P點橫坐標代入直線和拋物線解析式,可得其縱坐標表達式;
(3)先假設存在點P,根據四邊形DCEP是平行四形的條件進行推理,若能求出P點坐標,則證明存在點P,否則P點不存在.
試題解析:(1)把A(3,4)代入
得m=1,
∴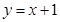 ,
,
∴B(0,1),
設二次函數解析式為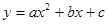 ,
,
把A.B.C三點坐標代入得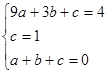
解得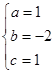
∴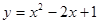 ;
;
(2)∵P點在直線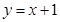 的圖象上,
的圖象上,
∴P點坐標為( ,
,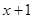 ),
),
∵E點在拋物線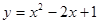 的圖象上,
的圖象上,
∴E點坐標為( ,
,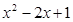 ),
),
∴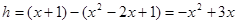 ;
;
(3)存在.
易求D點坐標為(1,2),則DC="2" ,
當PE=2時,PE∥DC,四邊形DCEP為平行四邊形,
即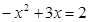 解得
解得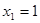 ,
,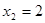 ,
,
當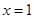 時,PE與DC重合,
時,PE與DC重合,
當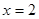 時,代入
時,代入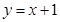 ,
,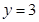
∴ P點坐標為(2,3).
考點:二次函數綜合題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
某農戶生產經銷一種農副產品,已知這種產品的成本價為20元/千克.市場調查發現,該產品每天的銷售量w (千克)與銷售價x (元/千克)有如下關系:w=﹣2x+80.設這種產品每天的銷售利潤為y (元).
(1)求y與x之間的函數關系式,自變量x的取值范圍;
(2)當銷售價定為多少元時,每天的銷售利潤最大?最大利潤是多少?
(3)如果物價部門規定這種產品的銷售價不得高于28元/千克,該農戶想要每天獲得150元的銷售利潤,銷售價應定為多少元?(參考關系:銷售額=售價×銷量,利潤=銷售額﹣成本)
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知二次函數 的圖象經過點A(2,-3),B(-1,0).
的圖象經過點A(2,-3),B(-1,0).
(1)求二次函數的解析式;
(2)觀察函數圖象,要使該二次函數的圖象與 軸只有一個交點,應把圖象沿
軸只有一個交點,應把圖象沿 軸向上平移幾個單位?
軸向上平移幾個單位?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平面直角坐標系中,已知拋物線 交
交 軸于A(2,0),B(6,0)兩點,交
軸于A(2,0),B(6,0)兩點,交 軸于點C(0,
軸于點C(0,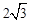 ).
).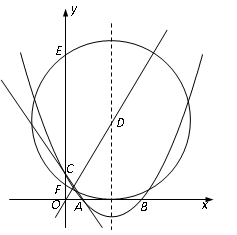
(1)求此拋物線的解析式;
(2)若此拋物線的對稱軸與直線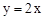 交于點D,作⊙D與x軸相切,⊙D交
交于點D,作⊙D與x軸相切,⊙D交 軸于點E、F兩點,求劣弧EF所對圓心角的度數;
軸于點E、F兩點,求劣弧EF所對圓心角的度數;
(3)P為此拋物線在第二象限圖像上的一點,PG垂直于 軸,垂足為點G,試確定P點的位置,使得△PGA的面積被直線AC分為1︰2兩部分.
軸,垂足為點G,試確定P點的位置,使得△PGA的面積被直線AC分為1︰2兩部分.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
正常水位時,拋物線拱橋下的水面寬為BC=20m,水面上升3m達到該地警戒水位DE時,橋下水面寬為10m.若以BC所在直線為x軸,BC的垂直平分線為y軸,建立如圖所示的平面直角坐標系.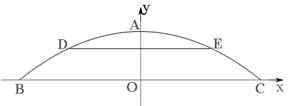
(1)求橋孔拋物線的函數關系式;
(2)如果水位以0.2m/h的速度持續上漲,那么達到警戒水位后,再過多長時間此橋孔將被淹沒;
(3)當達到警戒水位時,一艘裝有防汛器材的船,露出水面部分的寬為4m,高為0.75m,通過計算說明該船能否順利通過此拱橋?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
在某市開展的環境創優活動中,某居民小區要在一塊靠墻(墻長15米)的空地上修建一個矩形花園ABCD,花園的一邊靠墻,另三邊用總長為40m的柵欄圍成,若設花園與墻平行的一邊長為x(m),花園的面積為y(m2)。
(1)求y與x之間的函數關系式,并寫出自變量x的取值范圍;
(2)滿足條件的花園面積能達到200m2嗎?若能,求出此時x的值,若不能,說明理由:
(3)根據(1)中求得的函數關系式,判斷當x取何值時,花園的面積最大?最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
在平面直角坐標系xOy中,二次函數y=-x2+(m-1)x+4m的圖象與x軸負半軸交于點A,與y軸交于點B(0,4),已知點E(0,1).
(1)求m的值及點A的坐標;
(2)如圖,將△AEO沿x軸向右平移得到△A′E′O′,連結A′B、BE′.
①當點E′落在該二次函數的圖象上時,求AA′的長;
②設AA′=n,其中0<n<2,試用含n的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值時點E′的坐標;
③當A′B+BE′取得最小值時,求點E′的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
二次函數y=x2+bx+c的圖象經過點(4,3),(3,0).
(1)b= ,c= ;
(2)選取適當的數據填寫下表,并在右圖的直角坐標系中畫出該函數的圖像;
| x | … | | | | | | … |
| y | … | | | | | | … |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com