
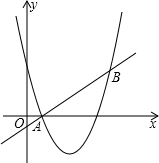
 直線y=x+a和拋物線y=x2+bx+c都經過A(1,0)、B(3,2)兩點,且不等式x+a>x2+bx+c 的整數解為K,若關于x的方程x2-(m2+5)x+2m2+6=0的兩實根之差的絕對值為n,且n滿足n=2(K+1),求m的值.
直線y=x+a和拋物線y=x2+bx+c都經過A(1,0)、B(3,2)兩點,且不等式x+a>x2+bx+c 的整數解為K,若關于x的方程x2-(m2+5)x+2m2+6=0的兩實根之差的絕對值為n,且n滿足n=2(K+1),求m的值.
|
| 5 |


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
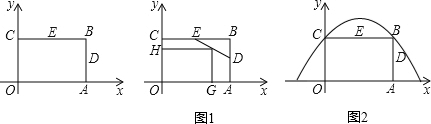
 (2012•濟南)如圖,濟南建邦大橋有一段拋物線型的拱梁,拋物線的表達式為y=ax2+bx.小強騎自行車從拱梁一端O沿直線勻速穿過拱梁部分的橋面OC,當小強騎自行車行駛10秒時和26秒時拱梁的高度相同,則小強騎自行車通過拱梁部分的橋面OC共需
(2012•濟南)如圖,濟南建邦大橋有一段拋物線型的拱梁,拋物線的表達式為y=ax2+bx.小強騎自行車從拱梁一端O沿直線勻速穿過拱梁部分的橋面OC,當小強騎自行車行駛10秒時和26秒時拱梁的高度相同,則小強騎自行車通過拱梁部分的橋面OC共需查看答案和解析>>
科目:初中數學 來源: 題型:
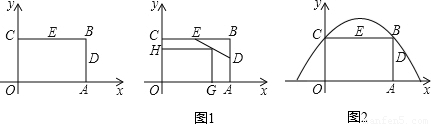
 如圖,濟南建邦大橋有一段拋物線型的拱梁,拋物線的表達式為y=ax2+bx.小強騎自行車從拱梁一端O沿直線勻速穿過拱梁部分的橋面OC,當小強騎自行車行駛10秒時和26秒時拱梁的高度相同,則小強騎自行車通過拱梁部分的橋面OC共需
如圖,濟南建邦大橋有一段拋物線型的拱梁,拋物線的表達式為y=ax2+bx.小強騎自行車從拱梁一端O沿直線勻速穿過拱梁部分的橋面OC,當小強騎自行車行駛10秒時和26秒時拱梁的高度相同,則小強騎自行車通過拱梁部分的橋面OC共需查看答案和解析>>
科目:初中數學 來源:第34章《二次函數》中考題集(40):34.4 二次函數的應用(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2011-2012學年廣西省貴港市九年級第一次教學質量監測數學卷 題型:解答題
(本題滿分12分)
如圖所示,在平面直角坐標系中,頂點為(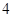 ,
,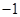 )的拋物線交
)的拋物線交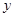 軸于
軸于 點,交
點,交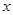 軸于
軸于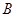 ,
,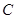 兩點(點
兩點(點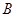 在點
在點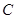 的左側),
已知
的左側),
已知 點坐標為(
點坐標為( ,
,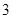 ).
).
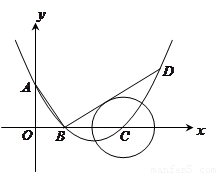
(1)求此拋物線的解析式;
(2)過點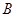 作線段
作線段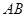 的垂線交拋物線于點
的垂線交拋物線于點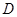 ,
,
如果以點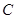 為圓心的圓與直線
為圓心的圓與直線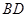 相切,請判斷拋物
相切,請判斷拋物
線的對稱軸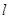 與⊙
與⊙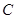 有怎樣的位置關系,并給出證明;
有怎樣的位置關系,并給出證明;
(3)已知點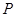 是拋物線上的一個動點,且位于
是拋物線上的一個動點,且位于 ,
,
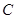 兩點之間,問:當點
兩點之間,問:當點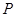 運動到什么位置時,
運動到什么位置時,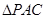 的
的
面積最大?并求出此時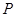 點的坐標和
點的坐標和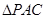 的最大面積.
的最大面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com