
如圖所示,直線AB∥CD,直線AB、CD被直線EF所截,EG平分∠BEF,FG平分∠DFE。
(1)若∠AEF=500,求∠EFG的度數。(4分)
(2)判斷EG與FG的位置關系,并說明理由。(6分)
(1)25°。(2)可證明∠G=180°-(∠BEF+∠DFE)=90°,所以EG⊥FG
解析試題分析:.解:(!)∵AB∥CD
∴∠EFD=∠AEF=50°
∵FG平分∠DFE
∵∠EFG= ∠DFE=
∠DFE= ×50°=25°
×50°=25°
(2)EG⊥FG
理由:∵AB∥CD
∴∠BEF+∠EFD=180°
∵EG平分∠BEF,FG平分∠DFE
∴∠GEF= ∠BEF,∠GFE=
∠BEF,∠GFE= ∠DFE
∠DFE
∴∠GEF+∠GFE= ∠BEF+
∠BEF+ ∠DFE
∠DFE
= (∠BEF+∠DFE)
(∠BEF+∠DFE)
= ×180°
×180°
=90°
∴∠G=180°-(∠BEF+∠DFE)=90°
∴EG⊥FG
考點:平行線性質與垂線判定
點評:本題難度中等,主要考查學生對平行線性質及垂線性質定理判定等應用。為中考常考題型,注意數形結合應用。


科目:初中數學 來源: 題型:解答題
小明在學習三角形知識時,發現如下三個有趣的結論:在Rt△ABC中,∠A=90°,BD平分∠ABC,M為直線AC上一點,ME⊥BC,垂足為E,∠AME的平分線交直線AB于點F.
(1)如圖①,M為邊AC上一點,則BD、MF的位置關系是 ;
如圖②,M為邊AC反向延長線上一點,則BD、MF的位置關系是 ;
如圖③,M為邊AC延長線上一點,則BD、MF的位置關系是 ;
(2)請就圖①、圖②、或圖③中的一種情況,給出證明.
我選圖 來證明.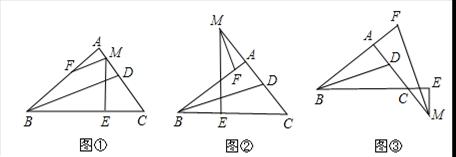
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
(1)如圖,直線l 、l
、l 分別與直線l
分別與直線l 、l
、l 相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度數.
相交,∠1=76°,∠2=104°,∠3=68°,求∠4的度數.
(2)如圖,∠1+∠2=180°,∠3=∠B,試判斷∠AED與∠ACB的大小關系,并對此結論進行證明.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知△ABC和點O.
(1)把△ABC繞點O順時針旋轉900得到△A1B1C1,在網格中畫出△A1B1C1;
(2)用直尺和圓規作△ABC的邊AB,AC的垂直平分線,并標出兩條垂直平分線的交點P(要求保留作圖痕跡,不寫作法);指出點P是△ABC的內心,外心,還是重心?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖所示的正方形網格中,△ABC的頂點均在格點上,請在所給直角坐標系中按要求畫圖和解答下列問題:
(1)以A點為旋轉中心,將△ABC繞點A順時針旋轉 得△AB1C1,畫出△AB1C1.
得△AB1C1,畫出△AB1C1.
(2)作出△ABC關于坐標原點O成中心對稱的△A2B2C2.
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
在比例尺是1∶8 000的南京市城區地圖上,太平南路的長度約為25 cm,它的實際長度約為( )
| A.320 cm | B.320 m |
| C.2 000 cm | D.2 000 m |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com