
如圖,在平面直角坐標(biāo)系中,頂點(diǎn)為(4,1)的拋物線交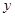 軸于點(diǎn)
軸于點(diǎn) ,交
,交 軸于
軸于 ,
, 兩點(diǎn)(點(diǎn)
兩點(diǎn)(點(diǎn) 在點(diǎn)
在點(diǎn) 的左側(cè)),已知
的左側(cè)),已知 點(diǎn)坐標(biāo)為(6,0).
點(diǎn)坐標(biāo)為(6,0).
(1)求此拋物線的解析式;
(2)聯(lián)結(jié)AB,過點(diǎn) 作線段
作線段 的垂線交拋物線于點(diǎn)
的垂線交拋物線于點(diǎn) ,如果以點(diǎn)
,如果以點(diǎn) 為圓心的圓與拋物線的對稱軸
為圓心的圓與拋物線的對稱軸 相切,先補(bǔ)全圖形,再判斷直線
相切,先補(bǔ)全圖形,再判斷直線 與⊙
與⊙ 的位置關(guān)系并加以證明;
的位置關(guān)系并加以證明;
(3)已知點(diǎn) 是拋物線上的一個動點(diǎn),且位于
是拋物線上的一個動點(diǎn),且位于 ,
, 兩點(diǎn)之間.問:當(dāng)點(diǎn)
兩點(diǎn)之間.問:當(dāng)點(diǎn) 運(yùn)動到什么位置時,
運(yùn)動到什么位置時, 的面積最大?求出
的面積最大?求出 的最大面積.
的最大面積.
(1)拋物線的解析式為 ;
;
(2)直線BD與⊙ 相離;
相離;
(3) 的最大面積是
的最大面積是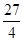 .
.
解析試題分析:(1)根據(jù)頂點(diǎn)坐標(biāo)列出頂點(diǎn)式,再將C點(diǎn)坐標(biāo)代入即可;
(2)先求出圓的半徑,再借助三角形相似,求出C到直線 的距離,比較他們的大小即可;
的距離,比較他們的大小即可;
(3)過點(diǎn) 作平行于
作平行于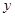 軸的直線交
軸的直線交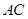 于點(diǎn)
于點(diǎn)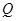 .設(shè)出
.設(shè)出 點(diǎn)坐標(biāo),求出PQ的值,再表示出
點(diǎn)坐標(biāo),求出PQ的值,再表示出 的面積,借助函數(shù)關(guān)系式求出最值.
的面積,借助函數(shù)關(guān)系式求出最值.
試題解析:(1)∵拋物線的頂點(diǎn)為(4,1),
∴設(shè)拋物線解析式為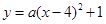 .
.
∵拋物線經(jīng)過點(diǎn) (6,0),
(6,0),
∴ .
.
∴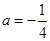 .
.
∴ .
.
所以拋物線的解析式為 ;
;
(2)補(bǔ)全圖形、判斷直線BD與⊙ 相離
相離
令 =0,則
=0,則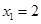 ,
,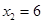 .
.
∴ 點(diǎn)坐標(biāo)(2,0).
點(diǎn)坐標(biāo)(2,0).
又∵拋物線交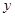 軸于點(diǎn)
軸于點(diǎn) ,
,
∴A點(diǎn)坐標(biāo)為(0,-3),
∴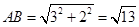 .
.
設(shè)⊙ 與對稱軸l相切于點(diǎn)F,則⊙
與對稱軸l相切于點(diǎn)F,則⊙ 的半徑CF=2,
的半徑CF=2,
作 ⊥BD于點(diǎn)E,則∠BEC=∠AOB=90°.
⊥BD于點(diǎn)E,則∠BEC=∠AOB=90°.
∵ ,
,
∴ .
.
又∵ ,
,
∴ .
.
∴ ∽
∽ ,
,
∴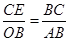 .
.
∴ ,
,
∴ .
.
∴直線BD與⊙ 相離;
相離;
(3)如圖,過點(diǎn) 作平行于
作平行于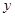 軸的直線交
軸的直線交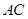 于點(diǎn)
于點(diǎn)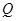 .
.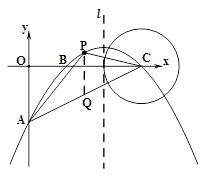
∵A(0,-3), (6,0).
(6,0).
∴直線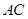 解析式為
解析式為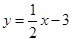 .
.
設(shè) 點(diǎn)坐標(biāo)為(
點(diǎn)坐標(biāo)為(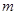 ,
, ),
),
則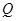 點(diǎn)的坐標(biāo)為(
點(diǎn)的坐標(biāo)為(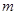 ,
,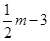 ).
).
∴PQ= -(
-(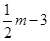 )=
)= .
.
∵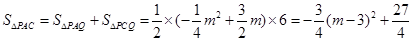 ,
,
∴當(dāng)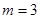 時,
時, 的面積最大為
的面積最大為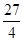
∵當(dāng)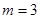 時,
時, =
=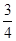
∴ 點(diǎn)坐標(biāo)為(3,
點(diǎn)坐標(biāo)為(3,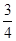 ).
).
綜上: 點(diǎn)的位置是(3,
點(diǎn)的位置是(3,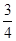 ),
), 的最大面積是
的最大面積是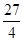 .
.
考點(diǎn):拋物線,圓,動點(diǎn)問題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,在平面直角坐標(biāo)系xOy中,拋物線y=ax2+bx+3的頂點(diǎn)為M(2,﹣1),交x軸與A、B兩點(diǎn),交y軸于點(diǎn)C,其中點(diǎn)B的坐標(biāo)為(3,0).
(1)求該拋物線的解析式;
(2)設(shè)經(jīng)過點(diǎn)C的直線與該拋物線的另一個交點(diǎn)為D,且直線CD和直線CA關(guān)于直線CB對稱,求直線CD的解析式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知二次函數(shù)y=x2–kx+k–1(k>2).
(1)求證:拋物線y=x2–kx+k-1(k>2)與x軸必有兩個交點(diǎn);
(2)拋物線與x軸交于A、B兩點(diǎn)(點(diǎn)A在點(diǎn)B的左側(cè)),與y軸交于點(diǎn)C,若 ,求拋物線的表達(dá)式;
,求拋物線的表達(dá)式;
(3)以(2)中的拋物線上一點(diǎn)P(m,n)為圓心,1為半徑作圓,直接寫出:當(dāng)m取何值時,x軸與 相離、相切、相交.
相離、相切、相交.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,二次函數(shù) 的圖象與x軸交于點(diǎn)A(-3,0)和點(diǎn)B,以AB為邊在x軸上方作正方形ABCD,點(diǎn)P是x軸上一動點(diǎn),連接DP,過點(diǎn)P作DP的垂線與y軸交于點(diǎn)E.
的圖象與x軸交于點(diǎn)A(-3,0)和點(diǎn)B,以AB為邊在x軸上方作正方形ABCD,點(diǎn)P是x軸上一動點(diǎn),連接DP,過點(diǎn)P作DP的垂線與y軸交于點(diǎn)E.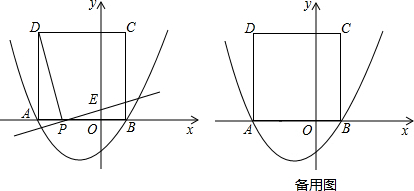
(1)請直接寫出點(diǎn)D的坐標(biāo):
(2)當(dāng)點(diǎn)P在線段AO(點(diǎn)P不與A、O重合)上運(yùn)動至何處時,線段OE的長有最大值,求出這個最大值;
(3)是否存在這樣的點(diǎn)P,使△PED是等腰三角形?若存在,請求出點(diǎn)P的坐標(biāo)及此時△PED與正方形ABCD重疊部分的面積;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
某公司銷售一種新型節(jié)能電子小產(chǎn)品,現(xiàn)準(zhǔn)備從國內(nèi)和國外兩種銷售方案中選擇一種進(jìn)行銷售:①若只在國內(nèi)銷售,銷售價格y(元/件)與月銷量x(件)的函數(shù)關(guān)系式為y=- x+150,成本為20元/件,月利潤為W內(nèi)(元);②若只在國外銷售,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數(shù),10≤a≤40),當(dāng)月銷量為x(件)時,每月還需繳納
x+150,成本為20元/件,月利潤為W內(nèi)(元);②若只在國外銷售,銷售價格為150元/件,受各種不確定因素影響,成本為a元/件(a為常數(shù),10≤a≤40),當(dāng)月銷量為x(件)時,每月還需繳納 x2元的附加費(fèi),月利潤為W外(元).
x2元的附加費(fèi),月利潤為W外(元).
(1)若只在國內(nèi)銷售,當(dāng)x=1000(件)時,y= (元/件);
(2)分別求出W內(nèi)、W外與x間的函數(shù)關(guān)系式(不必寫x的取值范圍);
(3)若在國外銷售月利潤的最大值與在國內(nèi)銷售月利潤的最大值相同,求a的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
小明利用暑假20天(8月5日至24日)參與了一家網(wǎng)店經(jīng)營的社會實(shí)踐.負(fù)責(zé)在網(wǎng)絡(luò)上銷售一種新款的SD卡,每張成本價為20元.第 天銷售的相關(guān)信息如下表所示.
天銷售的相關(guān)信息如下表所示.
| 銷售量p(張) |  |
| 銷售單價q(元/張) |  |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
在直角梯形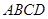 中,
中,  , 高
, 高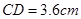 (如圖1). 動點(diǎn)
(如圖1). 動點(diǎn) 同時從點(diǎn)
同時從點(diǎn) 出發(fā), 點(diǎn)
出發(fā), 點(diǎn)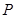 沿
沿 運(yùn)動到點(diǎn)
運(yùn)動到點(diǎn) 停止, 點(diǎn)
停止, 點(diǎn) 沿
沿 運(yùn)動到點(diǎn)
運(yùn)動到點(diǎn) 停止,兩點(diǎn)運(yùn)動時的速度都是1cm/s,而當(dāng)點(diǎn)
停止,兩點(diǎn)運(yùn)動時的速度都是1cm/s,而當(dāng)點(diǎn)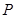 到達(dá)點(diǎn)
到達(dá)點(diǎn) 時,點(diǎn)
時,點(diǎn) 正好到達(dá)點(diǎn)
正好到達(dá)點(diǎn) . 設(shè)
. 設(shè) 同時從點(diǎn)
同時從點(diǎn) 出發(fā),經(jīng)過的時間為
出發(fā),經(jīng)過的時間為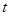 (s)時,
(s)時,  的面積為
的面積為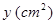 (如圖2). 分別以
(如圖2). 分別以 為橫、縱坐標(biāo)建立直角坐標(biāo)系, 已知點(diǎn)
為橫、縱坐標(biāo)建立直角坐標(biāo)系, 已知點(diǎn)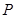 在
在 邊上從
邊上從 到
到 運(yùn)動時,
運(yùn)動時,  與
與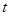 的函數(shù)圖象是圖3中的線段
的函數(shù)圖象是圖3中的線段 .
.

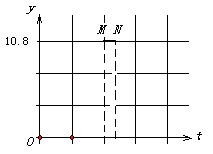
(圖1) (圖2) (圖3)
(1)分別求出梯形中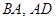 的長度;
的長度;
(2)分別寫出點(diǎn)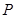 在
在 邊上和
邊上和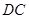 邊上運(yùn)動時,
邊上運(yùn)動時,  與
與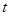 的函數(shù)關(guān)系式(注明自變量的取值范圍), 并在圖3中補(bǔ)全整個運(yùn)動中
的函數(shù)關(guān)系式(注明自變量的取值范圍), 并在圖3中補(bǔ)全整個運(yùn)動中 關(guān)于
關(guān)于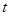 的函數(shù)關(guān)系的大致圖象.
的函數(shù)關(guān)系的大致圖象.
(3)問:是否存在這樣的t,使PQ將梯形ABCD的面積恰好分成1:6的兩部分?若存在,求出這樣的t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知二次函數(shù)y=x2+bx+c中,函數(shù)y與自變量x的部分對應(yīng)值如下表:
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
 ?
?查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,拋物線 與x軸交于A、C兩點(diǎn),與y軸交于B點(diǎn).
與x軸交于A、C兩點(diǎn),與y軸交于B點(diǎn).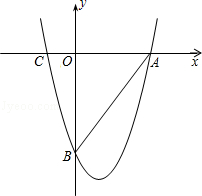
(1)求△AOB的外接圓的面積;
(2)若動點(diǎn)P從點(diǎn)A出發(fā),以每秒1個單位沿射線AC方向運(yùn)動;同時,點(diǎn)Q從點(diǎn)B出發(fā),以每秒0.5個單位沿射線BA方向運(yùn)動,當(dāng)點(diǎn)P到達(dá)點(diǎn)C處時,兩點(diǎn)同時停止運(yùn)動.問當(dāng)t為何值時,以A、P、Q為頂點(diǎn)的三角形與△OAB相似?
(3)若M為線段AB上一個動點(diǎn),過點(diǎn)M作MN平行于y軸交拋物線于點(diǎn)N.
問:是否存在這樣的點(diǎn)M,使得四邊形OMNB恰為平行四邊形?若存在,求出點(diǎn)M的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com