
如圖,在以AB為直徑的半圓中,有一個邊長為1的內接正方形CDEF,則以AC和BC的長為兩根的一元二次方程是( )
A. | B. |
C. | D. |
A.
解析試題分析:連接AD,BD,OD,由AB為直徑與四邊形DCFE是正方形,即可證得△ACD∽△DCB,則可求得AC•BC=DC2=1,又由勾股定理求得AB的值,即可得AC+BC=AB,根據根與系數的關系即可求得答案.
連接AD,BD,OD,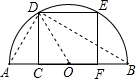
∵AB為直徑,
∴∠ADB=90°,
∵四邊形DCFE是正方形,
∴DC⊥AB,
∴∠ACD=∠DCB=90°,
∴∠ADC+∠CDB=∠A+∠ADC=90°,
∴∠A=∠CDB,
∴△ACD∽△DCB,
∴ ,
,
又∵正方形CDEF的邊長為1,
∵AC•BC=DC2=1,
∵AC+BC=AB,
在Rt△OCD中,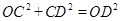 ,
,
∴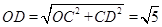 ,
,
∴AC+BC=AB=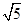 ,
,
以AC和BC的長為兩根的一元二次方程是
考點:(1)根與系數的關系;(2)勾股定理;(3)正方形的性質;(4)圓周角定理;(5)相似三角形的判定與性質.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:初中數學 來源: 題型:單選題
已知△ABC和△DEF相似,且△ABC的三邊長為3、4、5,如果△DEF的周長為6,那么下列不可能是△DEF一邊長的是( )
| A.1.5; | B.2; | C.2.5; | D.3. |
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
如圖,D是△ABC的邊BC上一點,已知AB=4,AD=2.∠DAC=∠B,若△ABD的面積為a,則△ACD的面積為( )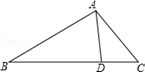
| A.a | B. | C. | D. |
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
如圖,△ABO縮小后變為△A′B′O,其中A、B的對應點分別為A′、B′,A′、B′均在圖中格點上,若線段AB上有一點P(m,n),則點P在A′B′上的對應點P′的坐標為
A、 B、(m,n) C、
B、(m,n) C、 D、
D、
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
兩地實際距離為2000米,圖上距離為2cm,則這張地圖的比例尺為( )
| A.1000:1 | B.100000:1 | C.1:1000 | D.1:100000 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com