
 的一元二次方程
的一元二次方程 .
. 取哪些整數時,x1、x2均為整數;
取哪些整數時,x1、x2均為整數; ,求k的值.
,求k的值. .
.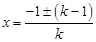 ,
, ,
,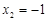 ,要使得方程的根為整數,只要要求
,要使得方程的根為整數,只要要求 是整數即可,進而只要要求
是整數即可,進而只要要求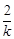 為整數,k是2的因數,所以k=±1或者k=±2;(3)方法一:由(2)可以得到
為整數,k是2的因數,所以k=±1或者k=±2;(3)方法一:由(2)可以得到  ,
,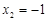 ,所以
,所以 ,分類討論,①當
,分類討論,①當 時,此方程無解;②當
時,此方程無解;②當 時,解得
時,解得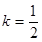 ;方法二:可以根據根與系數關系
;方法二:可以根據根與系數關系 ,
, 進行求解,具體詳見解析.
進行求解,具體詳見解析. 是關于x的一元二次方程,
是關于x的一元二次方程,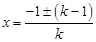 ,
, ,
,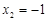 ,
, 為整數,即
為整數,即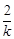 是整數,
是整數, ,
,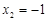 ,
, ,分類討論:
,分類討論: 時,此方程無解;
時,此方程無解; 時,解得
時,解得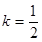 ;
; ,兩邊平方,有
,兩邊平方,有 ,
,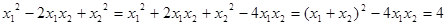 ,
, ,
, ,
,  ,
, .
.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
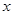 m,則根據題意可列方程為 __ .
m,則根據題意可列方程為 __ .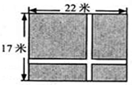
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com