
 從點
從點 出發,以每秒1個單位的速度沿
出發,以每秒1個單位的速度沿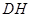 運動到點
運動到點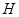 停止,在運動過程中,過點
停止,在運動過程中,過點 作
作 交折線
交折線 于點
于點 ,將紙片沿直線
,將紙片沿直線 折疊,點
折疊,點 、
、 的對應點分別是點
的對應點分別是點 、
、 。設
。設 點運動的時間是
點運動的時間是 秒(
秒( )。
)。 和點
和點 重合時,求運動時間
重合時,求運動時間 的值;
的值; 或四邊形
或四邊形 與梯形
與梯形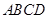 重疊部分面積為
重疊部分面積為 ,請直接寫出
,請直接寫出 與
與 之間的函數關系式和相應自變量
之間的函數關系式和相應自變量 的取值范圍;
的取值范圍; ,交線段
,交線段 于點
于點 ,交線段
,交線段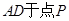 。在直線
。在直線 上存在點
上存在點 ,使
,使 為等腰直角三角形。請求出線段
為等腰直角三角形。請求出線段 的所有可能的長度。
的所有可能的長度。
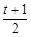 =
=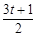
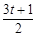 =
=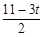 .∵等邊△PMN,MN=t+1,
.∵等邊△PMN,MN=t+1,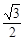 (t+1).
(t+1). .
.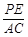 =
=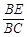 .
.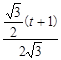 =
=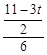 ,解得t=
,解得t=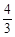
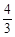 時,△PMN在△ABC內部.
時,△PMN在△ABC內部.
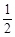 ×(t+1)×
×(t+1)×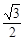 (t+1)=
(t+1)=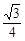 (t+1)2
(t+1)2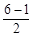 =
=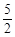 (秒)
(秒)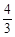 <t<
<t<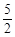 時,△PMN與△ABC重疊部分為四邊形EFNM.
時,△PMN與△ABC重疊部分為四邊形EFNM.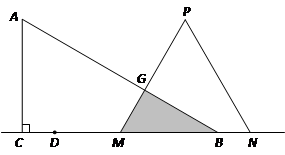
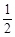 PF=
PF=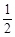 (3t-4),EF=
(3t-4),EF=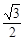 PF=
PF=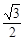 (3t-4).
(3t-4).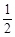 EF·PE=
EF·PE=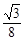 (3t-4)2
(3t-4)2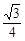 (t+1)2-
(t+1)2-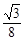 (3t-4)2
(3t-4)2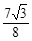 t2+
t2+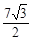 t-
t-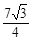 .
.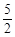 ≤t<6時,△PMN與△ABC重疊部分為△GMB.在Rt△GMB中,∠GBM=30°,MB=6-t.
≤t<6時,△PMN與△ABC重疊部分為△GMB.在Rt△GMB中,∠GBM=30°,MB=6-t.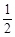 MB=
MB=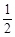 (6-t),GB=
(6-t),GB=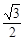 MB=
MB=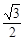 (6-t)
(6-t)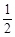 GM·GB=
GM·GB=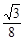 (6-t)2當t≥6時,S=0.
(6-t)2當t≥6時,S=0.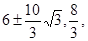
 與
與 之間的函數關系;
之間的函數關系;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源:不詳 題型:解答題
 經過點O(0,0),A(4,0),B(5,5),點C是y軸負半軸上一點,直線
經過點O(0,0),A(4,0),B(5,5),點C是y軸負半軸上一點,直線 經過B,C兩點,且
經過B,C兩點,且 .
.
 的解析式;
的解析式;查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
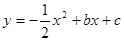 的圖象經過A(2,0)B(0,-6)兩點
的圖象經過A(2,0)B(0,-6)兩點
 軸交于點C,連結BA、BC,求△ABC的面積
軸交于點C,連結BA、BC,求△ABC的面積查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 中,
中, ,
, .它的頂點
.它的頂點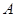 的坐標為
的坐標為 ,頂點
,頂點 的坐標為
的坐標為 ,
, ,點
,點 從點
從點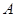 出發,沿
出發,沿 的方向勻速運動,同時點
的方向勻速運動,同時點 從點
從點 出發,沿
出發,沿 軸正方向以相同速度運動,當點
軸正方向以相同速度運動,當點 到達點
到達點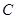 時,兩點同時停止運動,設運動的時間為
時,兩點同時停止運動,設運動的時間為 秒.
秒.
 的度數.
的度數. 在
在 上運動時,
上運動時, 的面積
的面積 (平方單位)與時間
(平方單位)與時間 (秒)之間的函數圖象為拋物線的一部分,(如圖②),求點
(秒)之間的函數圖象為拋物線的一部分,(如圖②),求點 的運動速度.
的運動速度. 與時間
與時間 之間的函數關系式及面積
之間的函數關系式及面積 取最大值時點
取最大值時點 的坐標.
的坐標. 保持(2)中的速度不變,那么點
保持(2)中的速度不變,那么點 沿
沿 邊運動時,
邊運動時,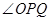 的大小隨著時間
的大小隨著時間 的增大而增大;沿著
的增大而增大;沿著 邊運動時,
邊運動時,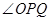 的大小隨著時間
的大小隨著時間 的增大而減小,當點
的增大而減小,當點 沿這兩邊運動時,使
沿這兩邊運動時,使 的點
的點 有幾個?請說明理由.
有幾個?請說明理由.查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
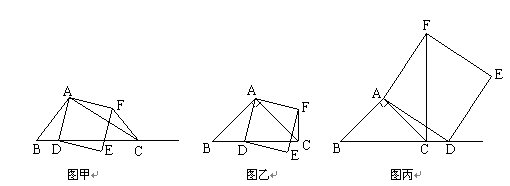
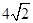 ,BC=3,在(2)的條件下,設正方形ADEF的邊DE與線段CF相交于點P,求線段CP長的最大值.
,BC=3,在(2)的條件下,設正方形ADEF的邊DE與線段CF相交于點P,求線段CP長的最大值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com