
如圖,在矩形ABCD中,AB=1,BC=3,點E為BC邊上的動點(點E與點B、C不重合),設BE=x.
操作:在射線BC上取一點F,使得EF=BE,以點F為直角頂點、EF為邊作等腰直角三角形EFG,設△EFG與矩形ABCD重疊部分的面積為S.
(1)求S與x的函數關系式,并寫出自變量x的取值范圍;
(2)S是否存在最大值?若存在,請直接寫出最大值,若不存在,請說明理由.
(1)①當0<x≤1時, S= EF•FG=
EF•FG= x2(0<x≤1);
x2(0<x≤1);
②當1<x≤1.5時,S= (MN+EF)FN=x﹣
(MN+EF)FN=x﹣ (1<x≤1.5);
(1<x≤1.5);
③當1.5<x≤2時,S= (MD+EC)CD=﹣x+
(MD+EC)CD=﹣x+ (1.5<x≤2)
(1.5<x≤2)
④當2<x<3時, S= CE•CM=
CE•CM= x2﹣3x+
x2﹣3x+ (2<x<3);
(2<x<3);
(2)存在,其最大值為1.
解析試題分析:(1)本題要分情況進行討論:
①當EF≤CD,即當0<x≤1時,重合部分是△EFG,兩直角邊的長均為x,由此可得出S,x的函數關系式.
②當CD<EF≤ BC,即當1<x≤1.5時,重合部分是個梯形,可用相似三角形求出梯形的上底的長,進而根據梯形的面積計算公式得出S,x的函數關系式.
BC,即當1<x≤1.5時,重合部分是個梯形,可用相似三角形求出梯形的上底的長,進而根據梯形的面積計算公式得出S,x的函數關系式.
③當EF> BC,但D在EG上或EG右側,即當1.5<x≤2時,此時重合部分是個梯形,如果設EG與AD相交于點M,AD的延長線與FG相交于點N,可先在相似三角形GMN和GEF中求出MN的長,而后根據MD=MN﹣DN求出梯形的上底長,進而可按梯形的面積計算公式得出S,x的函數關系式.
BC,但D在EG上或EG右側,即當1.5<x≤2時,此時重合部分是個梯形,如果設EG與AD相交于點M,AD的延長線與FG相交于點N,可先在相似三角形GMN和GEF中求出MN的長,而后根據MD=MN﹣DN求出梯形的上底長,進而可按梯形的面積計算公式得出S,x的函數關系式.
④當EF在D點右側時,即當2<x<3時,重合部分是個三角形,先用x表示出兩直角邊的長,然后按①的方法進行求解即可.
(2)按上面分析的四種情況,分別進行求解,得出不同自變量的取值范圍內S的最大值,然后進行比較即可得出S的最大值.
(1)①當0<x≤1時,FG=EF=x<1=AB(如圖1),
∴S= EF•FG=
EF•FG= x2(0<x≤1);
x2(0<x≤1);
②當1<x≤1.5時,FG=EF=x>1=AB(如圖2),
設EG與AD相交于點M,FG與AD相交于點N,
∵四邊形ABCD是矩形
∴AD∥BC
∴∠GNM=∠GEF=45°,∠GNM=∠GFE=90°
∴∠MGN=45°
∴MN=GN=x﹣1
S= (MN+EF)FN=x﹣
(MN+EF)FN=x﹣ (1<x≤1.5);
(1<x≤1.5);
③當1.5<x≤2時,(如圖3),設EG與AD相交于點M,AD的延長線與FG相交于點N,
∵四邊形ABCD是矩形
∴AN∥BF
同理MN=GN=x﹣1
∵∠FNM=∠GFE=∠DCF=90°
∴四邊形DCFN是矩形
DN=CF=BF﹣BC=2x﹣3,
MD=MN﹣DN=(x﹣1)﹣(2x﹣3)=2﹣x
S= (MD+EC)CD=﹣x+
(MD+EC)CD=﹣x+ (1.5<x≤2)
(1.5<x≤2)
④當2<x<3時,(如圖4),
設EG與CD相交于點M
∵四邊形ABCD是矩形,△EFG是等腰直角三角形,
∴∠MCE=90°,∠MEC=45°=∠CME
∴CM=CE=3﹣x
∴S= CE•CM=
CE•CM= x2﹣3x+
x2﹣3x+ (2<x<3);
(2<x<3);
(2)存在,其最大值為1.
考點:二次函數綜合題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
如圖,二次函數 的圖象交x軸于A(﹣1,0),B(2,0),交y軸于C(0,﹣2),過A,C畫直線.
的圖象交x軸于A(﹣1,0),B(2,0),交y軸于C(0,﹣2),過A,C畫直線.
(1)求二次函數的解析式;
(2)點P在x軸正半軸上,且PA=PC,求OP的長;
(3)點M在二次函數圖象上,以M為圓心的圓與直線AC相切,切點為H.
①若M在y軸右側,且△CHM∽△AOC(點C與點A對應),求點M的坐標;
②若⊙M的半徑為  ,求點M的坐標.
,求點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,二次函數 的圖象與
的圖象與 軸交于
軸交于 、
、 兩點,與
兩點,與 軸交于
軸交于 點,已知點
點,已知點 (-1,0),點C(0,-2).
(-1,0),點C(0,-2).
(1)求拋物線的函數解析式;
(2)試探究 的外接圓的圓心位置,并求出圓心坐標;
的外接圓的圓心位置,并求出圓心坐標;
(3)此拋物線上是否存在點P,使得以P、A、C、B為頂點的四邊形為梯形.若存在,請寫出所有符合條件的P點坐標;若不存在,請說明理由;
(4)若點 是線段
是線段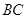 下方的拋物線上的一個動點,求
下方的拋物線上的一個動點,求 面積的最大值以及此時點
面積的最大值以及此時點 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知關于 的一元二次方程
的一元二次方程 有實數根,
有實數根, 為正整數.
為正整數.
(1)求 的值;
的值;
(2)當此方程有兩個不為0的整數根時,將關于 的二次函數
的二次函數 的圖象向下平移2個單位,求平移后的函數圖象的解析式;
的圖象向下平移2個單位,求平移后的函數圖象的解析式;
(3)在(2)的條件下,將平移后的二次函數圖象位于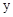 軸左側的部分沿
軸左側的部分沿 軸翻折,圖象的其余部分保持不變,得到一個新的圖象G.當直線
軸翻折,圖象的其余部分保持不變,得到一個新的圖象G.當直線 與圖象G有3個公共點時,請你直接寫出
與圖象G有3個公共點時,請你直接寫出 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線 交坐標軸于A、B、D三點,過點D作
交坐標軸于A、B、D三點,過點D作 軸的平行線交拋物線于點C.直線l過點E(0,-
軸的平行線交拋物線于點C.直線l過點E(0,-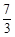 ),且平分梯形ABCD面積.
),且平分梯形ABCD面積.
⑴ 直接寫出A、B、D三點的坐標;
⑵ 直接寫出直線l的解析式;
⑶ 若點P在直線l上,且在x軸上方,tan∠OPB=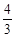 ,求點P的坐標.
,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,直角梯形OABC中,AB∥OC,點A坐標為(0,6),點C坐標為(3,0),BC= ,一拋物線過點A、B、 C.
,一拋物線過點A、B、 C.
(1)填空:點B的坐標為 ;
(2)求該拋物線的解析式;
(3)作平行于x軸的直線與x軸上方的拋物線交于點E 、F,以EF為直徑的圓恰好與x軸相切,求該圓的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,直線y= 與x軸交于點A,與y軸交于點C,以AC為直徑作⊙M,點
與x軸交于點A,與y軸交于點C,以AC為直徑作⊙M,點 是劣弧AO上一動點(
是劣弧AO上一動點( 點與
點與 不重合).拋物線y=-
不重合).拋物線y=- 經過點A、C,與x軸交于另一點B,
經過點A、C,與x軸交于另一點B,
(1)求拋物線的解析式及點B的坐標;
(2)在拋物線的對稱軸上是否存在一點P,是︱PA—PC︱的值最大;若存在,求出點P的坐標;若不存在,請說明理由。
(3)連 交
交 于點
于點 ,延長
,延長 至
至 ,使
,使 ,試探究當點
,試探究當點 運動到何處時,直線
運動到何處時,直線 與⊙M相切,并請說明理由.
與⊙M相切,并請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
某商場購進一批單價為50元的商品,規定銷售時單價不低于進價,每件的利潤不超過40%.其中銷售量y(件)與所售單價x(元)的關系可以近似的看作如圖所表示的一次函數.
(1)求y與x之間的函數關系式,并求出x的取值范圍;
(2)設該公司獲得的總利潤(總利潤=總銷售額-總成本)為w元,求w與x之間的函數關系式.當銷售單價為何值時,所獲利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com