
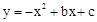 與直線
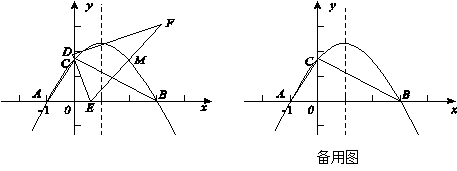
與直線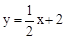 交于C,D兩點,其中點C在y軸上,點D的坐標為
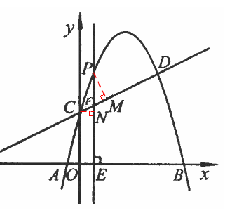
交于C,D兩點,其中點C在y軸上,點D的坐標為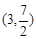 。點P是y軸右側的拋物線上一動點,過點P作
。點P是y軸右側的拋物線上一動點,過點P作 軸于點E,交CD于點F.
軸于點E,交CD于點F.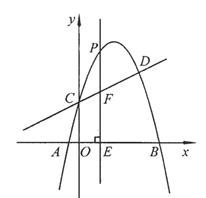
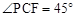 ,請直接寫出相應的點P的坐標
,請直接寫出相應的點P的坐標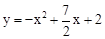 ;(2)當m=1或2或
;(2)當m=1或2或 時,以O,C,P,F為頂點的四邊形是平行四邊形,理由見解析;(3)P(
時,以O,C,P,F為頂點的四邊形是平行四邊形,理由見解析;(3)P(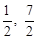 )或(
)或(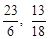 ).
).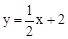 經過點C,求出點C的坐標;由拋物線
經過點C,求出點C的坐標;由拋物線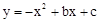 經過點C,D兩點,用待定系數法即可求出拋物線的解析式;(2)因為PF∥CO,所以當PF=CO時,以O,C,P,F為頂點的四邊形是平行四邊形,分
經過點C,D兩點,用待定系數法即可求出拋物線的解析式;(2)因為PF∥CO,所以當PF=CO時,以O,C,P,F為頂點的四邊形是平行四邊形,分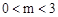 和
和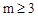 兩種情況討論即可;(3)如圖,當點P在CD上方且∠PCF=450時,作PM⊥CD于點M,CN⊥PF于點N,則△PMF∽△CNF,∴
兩種情況討論即可;(3)如圖,當點P在CD上方且∠PCF=450時,作PM⊥CD于點M,CN⊥PF于點N,則△PMF∽△CNF,∴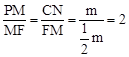 ,∴PM=CM=2CF,∴
,∴PM=CM=2CF,∴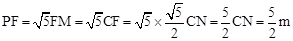 ,又∵
,又∵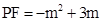 ,∴
,∴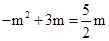 ,解得:
,解得: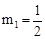 ,
,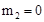 (舍去),∴P(
(舍去),∴P(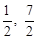 ),當點P在CD下方且∠PCF=450時,同理可以求得:另外一點為P(
),當點P在CD下方且∠PCF=450時,同理可以求得:另外一點為P(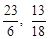 ).
).
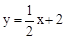 經過點C,∴C(0,2).
經過點C,∴C(0,2).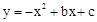 經過點C(0,2),D
經過點C(0,2),D 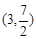 ,
,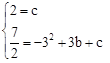 ,解得
,解得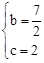 .
.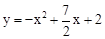 .
. .
.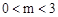 時,
時,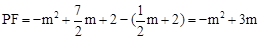 ,
, ,解得:
,解得: .
.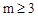 時,
時,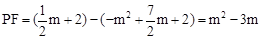 ,
,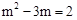 ,解得:
,解得: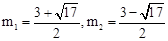 (∵點P在y軸右側的拋物線上,∴舍去).
(∵點P在y軸右側的拋物線上,∴舍去).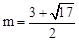 時,四邊形OCFP是平行四邊形.
時,四邊形OCFP是平行四邊形. 時,以O,C,P,F為頂點的四邊形是平行四邊形.
時,以O,C,P,F為頂點的四邊形是平行四邊形.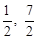 )或(
)或(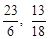 ).
).

 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| x | ﹣7 | ﹣6 | ﹣5 | ﹣4 | ﹣3 | ﹣2 |
| y | ﹣27 | ﹣13 | ﹣3 | 3 | 5 | 3 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 兩種產品,根據市場調研,發現如下信息:
兩種產品,根據市場調研,發現如下信息: 種產品所獲利潤
種產品所獲利潤 (萬元)與所售產品
(萬元)與所售產品 (噸)之間存在二次函數關系
(噸)之間存在二次函數關系 .當
.當 時,
時, ;當
;當 時,
時, .
. 種產品所獲利潤
種產品所獲利潤 (萬元)與所售產品
(萬元)與所售產品 (噸)之間存在正比例函數關系
(噸)之間存在正比例函數關系 .
. 兩種產品共10噸,請設計一個營銷方案,使銷售
兩種產品共10噸,請設計一個營銷方案,使銷售 兩種產品獲得的利潤之和最大,最大利潤是多少?
兩種產品獲得的利潤之和最大,最大利潤是多少?查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 .
.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
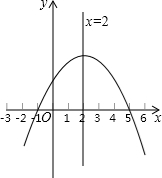
| A.ac<0 |
| B.a-b+c>0 |
| C.b=-4a |
| D.關于x的方程ax2+bx+c=0根是x1=-1,x2=5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com