
已知函數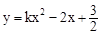 (
( 是常數)
是常數)
(1)若該函數的圖像與 軸只有一個交點,求
軸只有一個交點,求 的值;
的值;
(2)若點 在某反比例函數的圖像上,要使該反比例函數和二次函數
在某反比例函數的圖像上,要使該反比例函數和二次函數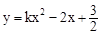 都是
都是 隨
隨 的增大而增大,求
的增大而增大,求 應滿足的條件以及
應滿足的條件以及 的取值范圍;
的取值范圍;
(3)設拋物線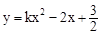 與
與 軸交于
軸交于 兩點,且
兩點,且 ,
, ,在
,在 軸上,是否存在點P,使△ABP是直角三角形?若存在,求出點P及△ABP的面積;若不存在,請說明理由。
軸上,是否存在點P,使△ABP是直角三角形?若存在,求出點P及△ABP的面積;若不存在,請說明理由。
解:(1)①當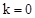 時,函數為
時,函數為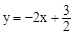 為一次函數,它的圖像與x軸只有一個交點。
為一次函數,它的圖像與x軸只有一個交點。
②當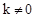 時,若函數
時,若函數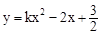 的圖像與x軸只有一個交點,則方程
的圖像與x軸只有一個交點,則方程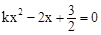 有兩個相等的實數根,所以
有兩個相等的實數根,所以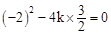 ,解得
,解得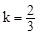 。
。
綜上所述,若函數的圖像與x軸只有一個交點,則 的值為0或
的值為0或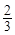 。
。
(2)設反比例函數為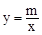 ,
,
∵點 在反比例函數的圖像上,∴
在反比例函數的圖像上,∴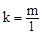 ,即
,即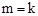 .。
.。
∴反比例函數為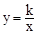 。
。
∵要使該反比例函數y隨著x的增大而增大,則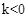 。
。
∵二次函數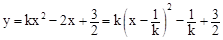 的對稱軸為
的對稱軸為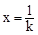 ,
,
∴要使二次函數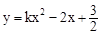 的y隨著x的增大而增大,在
的y隨著x的增大而增大,在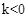 的情況下,x必須在對稱軸的左邊,即
的情況下,x必須在對稱軸的左邊,即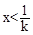 。
。
綜上所述,要使該反比例函數和二次函數都y隨著x的增大而增大,必須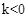 且
且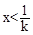 。
。
(3)存在。
∵拋物線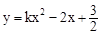 與x軸有兩個交點,
與x軸有兩個交點,
∴一元二次方程方程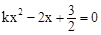 的判別式
的判別式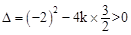 ,解得
,解得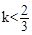 。
。
又∵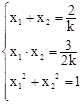 ,∴
,∴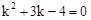 ,解得
,解得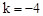 或
或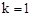 。
。
又∵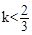 ,∴
,∴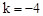 。
。
∴二次函數為 。
。
設P(0,p)是滿足條件的點,則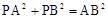 ,即
,即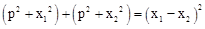 。
。
∴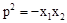 。∴
。∴ 。∴
。∴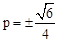 。
。
∴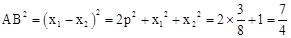 。∴
。∴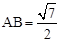 。
。
∴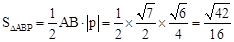 。
。
∴在y軸上,存在點P(0,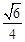 )或(0,
)或(0,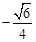 ),使△ABP是直角三角形,△ABP的面積為
),使△ABP是直角三角形,△ABP的面積為 。
。
解析


科目:初中數學 來源: 題型:解答題
矩形紙片ABCD中,AB=5,AD=4.
(1)如圖1,四邊形MNEF是在矩形紙片ABCD中裁剪出的一個正方形.你能否在該矩形中裁剪出一個面積最大的正方形,最大面積是多少?說明理由;
(2)請用矩形紙片ABCD剪拼成一個面積最大的正方形.要求:在圖2的矩形ABCD中畫出裁剪線,并在網格中畫出用裁剪出的紙片拼成的正方形示意圖(使正方形的頂點都在網格的格點上).
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,正方形AOCB在平面直角坐標系 中,點O為原點,點B在反比例函數
中,點O為原點,點B在反比例函數 (
( >
> )圖象上,△BOC的面積為
)圖象上,△BOC的面積為 .
.
(1)求反比例函數 的關系式;
的關系式;
(2)若動點E從A開始沿AB向B以每秒1個單位的速度運動,同時動點F 從B開始沿BC向C以每秒 個單位的速度運動,當其中一個動點到達端點時,另一個動點隨之停止運動.若運動時間用t表示,△BEF的面積用
個單位的速度運動,當其中一個動點到達端點時,另一個動點隨之停止運動.若運動時間用t表示,△BEF的面積用 表示,求出S關于t的函數關系式,并求出當運動時間t取何值時,△BEF的面積最大?
表示,求出S關于t的函數關系式,并求出當運動時間t取何值時,△BEF的面積最大?
(3)當運動時間為 秒時,在坐標軸上是否存在點P,使△PEF的周長最小?若存在,請求出點P的坐標;若不存在,請說明理由.
秒時,在坐標軸上是否存在點P,使△PEF的周長最小?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線y=ax2+bx+c(a≠0)的圖象過點C(0,1),頂點為Q(2,3),點D在x軸正半軸上,且OD=OC.
(1)求直線CD的解析式;
(2)求拋物線的解析式;
(3)將直線CD繞點C逆時針方向旋轉45°所得直線與拋物線相交于另一點E,求證:△CEQ∽△CDO;
(4)在(3)的條件下,若點P是線段QE上的動點,點F是線段OD上的動點,問:在P點和F點移動過程中,△PCF的周長是否存在最小值?若存在,求出這個最小值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平面直角坐標系中有一矩形ABCO(O為原點),點A、C分別在x軸、y軸上,且C點坐標為(0,6),將△BCD沿BD折疊(D點在OC邊上),使C點落在DA邊的E點上,并將△BAE沿BE折疊,恰好使點A落在BD邊的F點上.
(1)求BC的長,并求折痕BD所在直線的函數解析式;
(2)過點F作FG⊥x軸,垂足為G,FG的中點為H,若拋物線 經過B,H, D三點,求拋物線解析式;
經過B,H, D三點,求拋物線解析式;
(3)點P是矩形內部的點,且點P在(2)中的拋物線上運動(不含B, D點),過點P作PN⊥BC,分別交BC 和 BD于點N, M,是否存在這樣的點P,使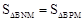 如果存在,求出點P的坐標;如果不存在,請說明理由.
如果存在,求出點P的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知拋物線y1=ax2+bx+c(a≠0)的頂點坐標是(1,4),它與直線y2=x+1的一個交點的橫坐標為2.
(1)求拋物線的解析式;
(2)在給出的坐標系中畫出拋物線y1=ax2+bx+c(a≠0)及直線y2=x+1的圖象,并根據圖象,直接寫出使得y1≥y2的x的取值范圍;
(3)設拋物線與x軸的右邊交點為A,過點A作x軸的垂線,交直線y2=x+1于點B,點P在拋物線上,當S△PAB≤6時,求點P的橫坐標x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
在平面直角坐標系中,已知M1(3,2),N1(5,﹣1),線段M1N1平移至線段MN處(注:M1與M,N1與N分別為對應點).
(1)若M(﹣2,5),請直接寫出N點坐標.
(2)在(1)問的條件下,點N在拋物線 上,求該拋物線對應的函數解析式.
上,求該拋物線對應的函數解析式.
(3)在(2)問條件下,若拋物線頂點為B,與y軸交于點A,點E為線段AB中點,點C(0,m)是y軸負半軸上一動點,線段EC與線段BO相交于F,且OC:OF=2: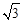 ,求m的值.
,求m的值.
(4)在(3)問條件下,動點P從B點出發,沿x軸正方向勻速運動,點P運動到什么位置時(即BP長為多少),將△ABP沿邊PE折疊,△APE與△PBE重疊部分的面積恰好為此時的△ABP面積的 ,求此時BP的長度.
,求此時BP的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
將矩形OABC置于平面直角坐標系中,點A的坐標為(0,4),點C的坐標為(m,0)(m>0),點D(m,1)在BC上,將矩形OABC沿AD折疊壓平,使點B落在坐標平面內,設點B的對應點為點E.
(1)當m=3時,點B的坐標為 ,點E的坐標為 ;
(2)隨著m的變化,試探索:點E能否恰好落在x軸上?若能,請求出m的值;若不能,請說明理由.
(3)如圖,若點E的縱坐標為-1,拋物線 (a≠0且a為常數)的頂點落在△ADE的內部,求a的取值范圍.
(a≠0且a為常數)的頂點落在△ADE的內部,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知:△ABC為邊長是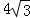 的等邊三角形,四邊形DEFG為邊長是6的正方形.現將等邊△ABC和正方形DEFG按如圖1的方式擺放,使點C與點E重合,點B、C(E)、F在同一條直線上,△ABC從圖1的位置出發,以每秒1個單位長度的速度沿EF方向向右勻速運動,當點C與點F重合時暫停運動,設△ABC的運動時間為t秒(t≥0).
的等邊三角形,四邊形DEFG為邊長是6的正方形.現將等邊△ABC和正方形DEFG按如圖1的方式擺放,使點C與點E重合,點B、C(E)、F在同一條直線上,△ABC從圖1的位置出發,以每秒1個單位長度的速度沿EF方向向右勻速運動,當點C與點F重合時暫停運動,設△ABC的運動時間為t秒(t≥0).
(1)在整個運動過程中,設等邊△ABC和正方形DEFG重疊部分的面積為S,請直接寫出S與t之間的函數關系式;
(2)如圖2,當點A與點D重合時,作∠ABE的角平分線BM交AE于M點,將△ABM繞點A逆時針旋轉,使邊AB與邊AC重合,得到△ACN.在線段AG上是否存在H點,使得△ANH為等腰三角形.如果存在,請求出線段EH的長度;若不存在,請說明理由.
(3)如圖3,若四邊形DEFG為邊長為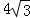 的正方形,△ABC的移動速度為每秒
的正方形,△ABC的移動速度為每秒 個單位長度,其余條件保持不變.△ABC開始移動的同時,Q點從F點開始,沿折線FG﹣GD以每秒
個單位長度,其余條件保持不變.△ABC開始移動的同時,Q點從F點開始,沿折線FG﹣GD以每秒 個單位長度開始移動,△ABC停止運動時,Q點也停止運動.設在運動過程中,DE交折線BA﹣AC于P點,則是否存在t的值,使得PC⊥EQ,若存在,請求出t的值;若不存在,請說明理由.
個單位長度開始移動,△ABC停止運動時,Q點也停止運動.設在運動過程中,DE交折線BA﹣AC于P點,則是否存在t的值,使得PC⊥EQ,若存在,請求出t的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com