
科目:初中數學 來源: 題型:閱讀理解
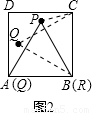
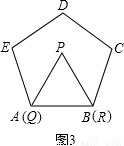
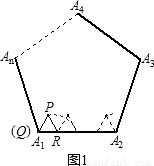
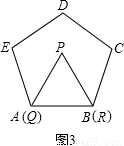
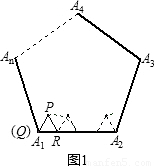
 27、閱讀:我們把邊長為1的等邊三角形PQR沿著邊長為整數的正n(n>3)邊形的邊按照如圖1的方式連續轉動,當頂點P回到正n邊形的內部時,我們把這種狀態稱為它的“點回歸”;當△PQR回到原來的位置時,我們把這種狀態稱為它的“三角形回歸”.
27、閱讀:我們把邊長為1的等邊三角形PQR沿著邊長為整數的正n(n>3)邊形的邊按照如圖1的方式連續轉動,當頂點P回到正n邊形的內部時,我們把這種狀態稱為它的“點回歸”;當△PQR回到原來的位置時,我們把這種狀態稱為它的“三角形回歸”.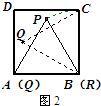

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
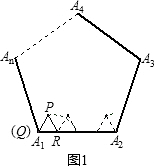 閱讀:我們把邊長為1的等邊三角形PQR沿著邊長為整數的正n(n>3)邊形的邊按照如圖1的方式連續轉動,當頂點P回到正n邊形的內部時,我們把這種狀態稱為它的“點回歸”;當△PQR回到原來的位置時,我們把這種狀態稱為它的“三角形回歸”.
閱讀:我們把邊長為1的等邊三角形PQR沿著邊長為整數的正n(n>3)邊形的邊按照如圖1的方式連續轉動,當頂點P回到正n邊形的內部時,我們把這種狀態稱為它的“點回歸”;當△PQR回到原來的位置時,我們把這種狀態稱為它的“三角形回歸”.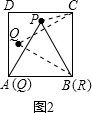
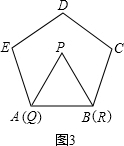
查看答案和解析>>
科目:初中數學 來源:江蘇期末題 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2009-2010學年九年級(上)期中數學試卷二(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com