已知二次函數圖像與y軸交于點（0，-4），并經過（-1，-6）和（1,2）
（1）求這個二次函數的解析式；
（2）求出這個函數的圖像的開口方向，對稱軸和頂點坐標；
（3）該函數圖像與x軸的交點坐標 .
科目：初中數學 來源： 題型：解答題
如圖,拋物線
（b,c是常數,且c＜0）與
軸分別交于點A、B（點A位于點B的左側）,與
軸的負半軸交于點C,點A的坐標為(－1,0)．
（1）請直接寫出點OA的長度;
（2）若常數b,c滿足關系式：
．求拋物線的解析式．
（3）在（2）的條件下,點P是軸下方拋物線上的動點,連接PB、PC．設△PBC的面積為S．
①求S的取值范圍;
②若△PBC的面積S為整數,則這樣的△PBC共有多少個（直接寫出結果）？
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
已知關于x的方程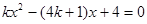
．
（1）當k取何值時，方程有兩個實數根；
（2）若二次函數
的圖象與
軸兩個交點的橫坐標均為整數，且k為正整數，求k值并用配方法求出拋物線的頂點坐標；
（3）若（2）中的拋物線與x軸交于A、B兩點，與y軸交于C點．將拋物線向上平移n個單位，使平移后得到的拋物線的頂點落在△ABC的內部（不包括△ABC的邊界），寫出n的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
天貓商城旗艦店銷售一種進價為每件20元的護眼臺燈．銷售過程中發現，每月銷售量y（件）與銷售單價x（元）之間的關系可近似的看作一次函數：
，在銷售過程中銷售單價不低于成本價，而每件的利潤不高于成本價的60%．
（1）設該旗艦店每月獲得利潤為w（元），求每月獲得利潤w（元）與銷售單價x（元）之間的函數關系式，并確定自變量x的取值范圍．
（2）當銷售單價定為多少元時，每月可獲得最大利潤？每月的最大利潤是多少？
（3）如果旗艦店想要每月獲得的利潤不低于2000元，那么每月的成本最少需要 元？
（成本＝進價×銷售量）
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
高科技發展公司投資500萬元，成功研制出一種市場需求量較大的高科技替代產品，并投入資金1500萬元作為固定投資，已知生產每件產品的成本是40元．在銷售過程中發現：當銷售單價定為100元時，年銷售量為20萬件；銷售單價每增加10元，年銷售量將減少1萬件，設銷售單價為x（元），年銷售量為y（萬件），年獲利（年獲利=年銷售額一生產成本—投資）為z（萬元）．
（1）試寫出y與x之間的函數關系式（不寫x的取值范圍）；
（2）試寫出z與x之間的函數關系式（不寫x的取值范圍）；
（3）公司計劃，在第一年按年獲利最大確定銷售單價進行銷售；到第二年年底獲利不低于1130萬元，請借助函數的大致圖象說明：第二年的銷售單價x（元）應確定在什么范圍內？
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
如圖,已知二次函數y=x2+bx+c過點A（1,0）,C（0,﹣3）
（1）求此二次函數的解析式；
（2）在拋物線上存在一點P使△ABP的面積為10,請直接寫出點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
已知：關于
的二次函數y=px2-(3p+2)x+2p+2(p>0）
（1）求證：無論p為何值時,此函數圖象與x軸總有兩個交點;
（2）設這兩個交點坐標分別為（x1,0）,（x2,0）（其中x1＜x2）且S=x2-2x1,求S關于P的函數解析式
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
如圖所示，直線l：y=3x+3與x軸交于點A，與y軸交于點B．把△AOB沿y軸翻折，點A落到點C，拋物線過點B、C和D（3，0）．
（1）求直線BD和拋物線的解析式．
（2）若BD與拋物線的對稱軸交于點M，點N在坐標軸上，以點N、B、D為頂點的三角形與△MCD相似，求所有滿足條件的點N的坐標．
（3）在拋物線上是否存在點P，使S△PBD=6？若存在，求出點P的坐標；若不存在，說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
;（2）向上, 
,
;（3）
和
.
確定開口方向,化為頂點式,求出對稱軸和頂點坐標;
,求解即可.
.
,解得
.
,∴這個函數的圖像的對稱軸為
,
軸的交點坐標.