
如圖,P1是反比例函數(shù) 在第一象限圖象上的一點,已知△P1O A1為等邊三角形,點A1的坐標(biāo)為(2,0).
在第一象限圖象上的一點,已知△P1O A1為等邊三角形,點A1的坐標(biāo)為(2,0).
(1)直接寫出點P1的坐標(biāo);
(2)求此反比例函數(shù)的解析式;
(3)若△P2A1A2為等邊三角形,求點A2的坐標(biāo).
(1)P1(1, );(2)
);(2) ;(3)(
;(3)(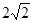 ,0).
,0).
解析試題分析:(1)由于△P1OA1為等邊三角形,作P1C⊥OA1,垂足為C,由等邊三角形的性質(zhì)及勾股定理可求出點P1的坐標(biāo);
(2)根據(jù)點P1是反比例函數(shù)y= (k>0)圖象上的一點,利用待定系數(shù)法求出此反比例函數(shù)的解析式;
(k>0)圖象上的一點,利用待定系數(shù)法求出此反比例函數(shù)的解析式;
(3)作P2D⊥A1A2,垂足為D.設(shè)A1D=a,由于△P2A1A2為等邊三角形,由等邊三角形的性質(zhì)及勾股定理,可用含a的代數(shù)式分別表示點P2的橫、縱坐標(biāo),再代入反比例函數(shù)的解析式中,求出a的值,進(jìn)而得出A2點的坐標(biāo).
試題解析:(1)P1(1, );
);
(2)∵P1在反比例函數(shù) (
(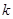 >0)圖象上,∴
>0)圖象上,∴ ,
,
∴ ,
,
∴反比例函數(shù)的解析式為 ;
;
(3)設(shè)等邊三角形P2 A1 A2的邊長為a(a>0),則A2(2+a,0).
如圖,過P2作P2H⊥x軸,垂足為點H. 
∴A1H=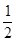 a,P2H= P2 A1sin∠P2A1H=a·sin600=
a,P2H= P2 A1sin∠P2A1H=a·sin600=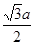 ,
,
∴P2(2+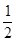 a,
a,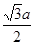 ).
).
∵ P2在反比例函數(shù) 圖象上,∴
圖象上,∴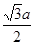 =
=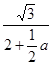 ,
,
即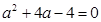 ,解得:
,解得: ,
, (舍去)
(舍去)
∴2+a=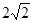 ,∴A2(
,∴A2(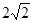 ,0)
,0)
考點: 反比例函數(shù)綜合題.


 名師伴你成長課時同步學(xué)練測系列答案
名師伴你成長課時同步學(xué)練測系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖所示,制作某種食品的同時需將原材料加熱,設(shè)該材料溫度為y ℃,從加熱開始計算的時間為x分鐘.據(jù)了解,該材料在加熱過程中溫度y與時間x成一次函數(shù)關(guān)系.已知該材料在加熱前的溫度為4℃,加熱一段時間使材料溫度達(dá)到28℃時停止加熱,停止加熱后,材料溫度逐漸下降,這時溫度y與時間x成反比例函數(shù)關(guān)系,已知當(dāng)?shù)?2分鐘時, 材料溫度是14℃.
(1)分別求出該材料加熱和停止加熱過程中y與x的函數(shù)關(guān)系式(寫出x的取值范圍);
(2)根據(jù)該食品制作要求,在材料溫度不低于12℃的這段時間內(nèi),需要對該材料進(jìn)行特殊處理,那么對該材料進(jìn)行特殊處理的時間為多少分鐘?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知:如圖,在平面直角坐標(biāo)系中,一次函數(shù) 的圖象與反比例函數(shù)
的圖象與反比例函數(shù) 的圖象交于一、三象限內(nèi)的A、B兩點,與x軸交于C點,點A的坐標(biāo)為(2,m),點B的坐標(biāo)為(n,
的圖象交于一、三象限內(nèi)的A、B兩點,與x軸交于C點,點A的坐標(biāo)為(2,m),點B的坐標(biāo)為(n, ),tan∠BOC
),tan∠BOC 。
。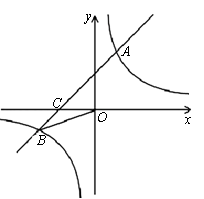
(l)求該反比例函數(shù)和一次函數(shù)的解析式;
(2)在x軸上有一點E(O點除外),使得△BCE與△BCO的面積相等,求出點E的坐標(biāo)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
(1)先求解下列兩題:
①如圖①,點B,D在射線AM上,點C,E在射線AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度數(shù);
②如圖②,在直角坐標(biāo)系中,點A在y軸正半軸上,AC∥x軸,點B,C的橫坐標(biāo)都是3,且BC=2,點D在AC上,且橫坐標(biāo)為1,若反比例函數(shù) (x>0)的圖象經(jīng)過點B,D,求k的值.
(x>0)的圖象經(jīng)過點B,D,求k的值.
(2)解題后,你發(fā)現(xiàn)以上兩小題有什么共同點?請簡單地寫出.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖, .
. 是反比例函數(shù)
是反比例函數(shù) (k>0)在第一象限圖象上的兩點,點
(k>0)在第一象限圖象上的兩點,點 的坐標(biāo)為(2,0),若△
的坐標(biāo)為(2,0),若△ 與△
與△ 均為等邊三角形.
均為等邊三角形.
(1)求此反比例函數(shù)的解析式;
(2)求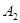 點的坐標(biāo).
點的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
已知y是x的反比例函數(shù),當(dāng)x=5時,y=8.
(1)求反比例函數(shù)解析式;
(2)求y=-10時x的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,點P1、P2、……Pn是反比例函數(shù)y= 在第一象限圖像上,點A1、A2……An在X軸上,若△P1OA1、△P2A1A2……△PnAN-1AN均為等腰直角三角形,則:
在第一象限圖像上,點A1、A2……An在X軸上,若△P1OA1、△P2A1A2……△PnAN-1AN均為等腰直角三角形,則:
(1)P1點的坐標(biāo)為
(2)求點A2與點P2的坐標(biāo);
(3)直接寫出點An與點Pn的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
如圖,直線l:y=x+1與x軸、y軸分別交于A、B兩點,點C與原點O關(guān)于直線l對稱.反比例函數(shù) 的圖象經(jīng)過點C,點P在反比例函數(shù)圖象上且位于C點左側(cè),過點P作x軸、y軸的垂線分別交直線l于M、N兩點.
的圖象經(jīng)過點C,點P在反比例函數(shù)圖象上且位于C點左側(cè),過點P作x軸、y軸的垂線分別交直線l于M、N兩點.
(1)求反比例函數(shù)的解析式;
(2)求AN•BM的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com