
 (2)
(2) ,
, ,
, .(3),當點
.(3),當點 的坐標是
的坐標是 時,
時,
 ,當點
,當點 的坐標是
的坐標是 時,
時, 

 ,
, ,
,
 ,
,
 是等腰三角形,且點
是等腰三角形,且點 在
在 軸的正半軸上,
軸的正半軸上,
 ,
,
 .
.
 .
. 的解析式為
的解析式為 ,
,
 ,
, .
. 直線
直線 的解析式為
的解析式為 .····················· 4分
.····················· 4分 拋物線
拋物線 關于
關于 軸對稱,
軸對稱, .············ 5分
.············ 5分
 經過
經過 ,
, 兩點.
兩點.
 解得
解得
 拋物線的解析式是
拋物線的解析式是 .······· 7分
.······· 7分 中,
中, ,易得
,易得 .
. 中,
中, ,
, ,易得
,易得 .
.
 是
是 的角平分線.
的角平分線. 直線
直線 與
與 軸關于直線
軸關于直線 對稱.
對稱. 關于直線
關于直線 的對稱點在
的對稱點在 軸上,則符合條件的點
軸上,則符合條件的點 就是直線
就是直線 與拋物線
與拋物線 的交點. 8分
的交點. 8分 點
點 在直線
在直線 :
: 上,
上, 的坐標是
的坐標是 .
.
 在拋物線
在拋物線 上,
上,
 .解得
.解得 ,
, .
. 的坐標是
的坐標是 ,
, .··············· 10分
.··············· 10分 的取值范圍,可先求
的取值范圍,可先求 的最小值.
的最小值. 的坐標是
的坐標是 時,點
時,點 與點
與點 重合,故
重合,故 .
. 的最小值就是點
的最小值就是點 到
到 軸的距離為
軸的距離為 ,
, 點
點 是
是 軸上的動點,
軸上的動點,
 無最大值,
無最大值,

 .···· 13分
.···· 13分 的坐標是
的坐標是 時,由點
時,由點 關于
關于 軸的對稱點
軸的對稱點 ,故只要求
,故只要求 的最小值,顯然線段
的最小值,顯然線段 最短.易求得
最短.易求得 .
.
 的最小值是6.
的最小值是6. 沒有最大值,
沒有最大值,
 的取值范圍是
的取值范圍是
 .
. 的坐標是
的坐標是 時,
時,
 ,
, 的坐標是
的坐標是 時,
時, 
 .··············· 15分
.··············· 15分 ,用待定系數法,由勾股定理得到點
,用待定系數法,由勾股定理得到點 ,而
,而 ,把它們代入即可
,把它們代入即可 對稱,則對稱軸
對稱,則對稱軸 ,再把點
,再把點 的坐標代入
的坐標代入 即可;由于點P關于直線AC的對稱點在x軸上,利用直角三角形三角函數,得出直線
即可;由于點P關于直線AC的對稱點在x軸上,利用直角三角形三角函數,得出直線 與
與 軸關于直線
軸關于直線 對稱,則符合條件的點
對稱,則符合條件的點 就是直線
就是直線 與拋物線
與拋物線 的交點,把
的交點,把 與
與 組成方程組,求方程組的解即可
組成方程組,求方程組的解即可 的坐標是
的坐標是 時,則
時,則 ,故最小值為
,故最小值為 ,但沒有最大值,故
,但沒有最大值,故
 ;當
;當 的坐標是
的坐標是 時,把點
時,把點 和點
和點 分到
分到 軸的兩側,兩點間連線最短,連線與
軸的兩側,兩點間連線最短,連線與 軸的交點就點
軸的交點就點 ,
, 的最小值是
的最小值是 ,同樣沒有最大值,故
,同樣沒有最大值,故



 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:初中數學 來源:不詳 題型:解答題
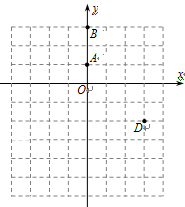
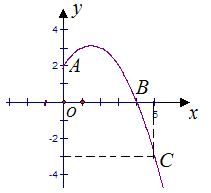
 經過點O(0,0),A(4,0),B(5,5),點C是y軸負半軸上一點,直線
經過點O(0,0),A(4,0),B(5,5),點C是y軸負半軸上一點,直線 經過B,C兩點,且
經過B,C兩點,且 .
.
 的解析式;
的解析式;查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
銷售單價 (元∕件) (元∕件) | …… | 30 | 40 | 50 | 60 | …… |
每天銷售量 (件) (件) | …… | 500 | 400 | 300 | 200 | …… |
 、
、 的各組對應值作為點的坐標,在下面的平面直角坐標系中描出相應的點,猜想
的各組對應值作為點的坐標,在下面的平面直角坐標系中描出相應的點,猜想 與
與 的函數關系,并求出函數關系式;
的函數關系,并求出函數關系式; 
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
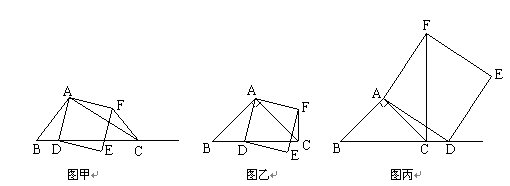
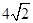 ,BC=3,在(2)的條件下,設正方形ADEF的邊DE與線段CF相交于點P,求線段CP長的最大值.
,BC=3,在(2)的條件下,設正方形ADEF的邊DE與線段CF相交于點P,求線段CP長的最大值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com