
(2011福建龍巖,25, 14分)如圖,在直角梯形ABCD中,∠D=∠BCD=90°,∠B=60°, AB=6,AD=9,
點E是CD上的一個動點(E不與D重合),過點E作EF∥AC,交AD于點F(當E運
動到C時,EF與AC重合巫臺).把△DEF沿EF對折,點D的對應點是點G,設DE=x,
△GEF與梯形ABCD重疊部分的面積為y。
(1) 求CD的長及∠1的度數;
(2) 若點G恰好在BC上,求此時x的值;
(3) 求y與x之間的函數關系式。并求x為何值時,y的值最大?最大值是多少?
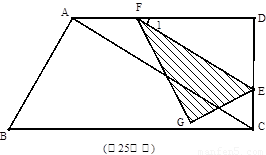
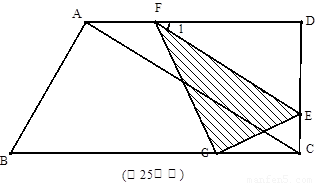
(1)CD=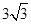 ∠1=30°
∠1=30°
(2)若點G恰好在BC上,
則有GE=DE=x,EC=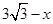
∵∠1=30°,∴∠FED=60°
∴∠GEF=60°
∴∠GEC=60°
∴GE=2CE
∴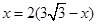
∴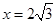
(3)∵△EFG≌△EFD
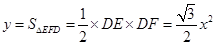
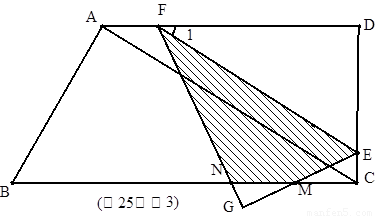
(1)當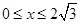 時,隨著x的增大,面積增大,此時△的面積就是重疊的面積,當
時,隨著x的增大,面積增大,此時△的面積就是重疊的面積,當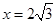 時,達到最大值,為
時,達到最大值,為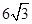 。
。
(2)當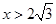 ,△EFG就有一部分在梯形外,如圖3,
,△EFG就有一部分在梯形外,如圖3,
∵GE=DE=x,EC=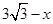
易求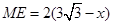 ,∴
,∴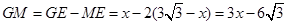
∴NG=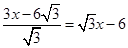
∴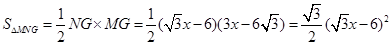
此時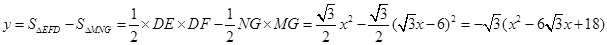
=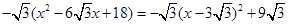
當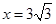 時,
時,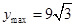
綜上所述。當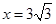 時,
時,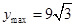 。
。
【解析】(1)過A做梯形的高,構造直角三角形,順用、逆用三角函數計算求解線段長和角度。
(2)化動為靜,抓住不同直角三角形邊角間的數量關系(從不同角度表示有特殊關系的線段),建立等量關系,解方程。
(3)分情況討論,求出x不同取值范圍下二次函數式的最值,比較得出。
【關鍵


科目:初中數學 來源: 題型:
| 環數 | 7 | 8 | 9 | 10 |
| 人數 | 4 | 2 | 3 | 1 |
| A.7.8環 | B.7.9環 | C.8.l環 | D.8.2環 |
查看答案和解析>>
科目:初中數學 來源:2011年福建省龍巖市中考數學試卷 題型:選擇題
.(2011福建龍巖,7,4分)數名射擊運動員第一輪比賽成績如下表所示;
|
環數 |
7 |
8 |
9 |
10 |
|
人數 |
4 |
2 |
3 |
1 |
則他們本輪比賽的平均成績是
A.7.8環 B.7.9環 C. 8.l環 D.8.2環
查看答案和解析>>
科目:初中數學 來源:2011年福建省龍巖市中考數學試卷 題型:選擇題
(2011福建龍巖,6,4分) 如圖.若乙、丙都在甲的北偏東70°方向上.乙在丁的正北方向上,
如圖.若乙、丙都在甲的北偏東70°方向上.乙在丁的正北方向上,
且乙到丙、丁的距離相同.則α的度數是
A.25° B.30° C.35° D.40°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com