
兩個直角邊為6的全等的等腰直角三角形Rt△AOB和Rt△CED,按如圖一所示的位置放置,點O與E重合.
(1)Rt△AOB固定不動,Rt△CED沿x軸以每秒2個單位長度的速度向右運動,當點E運動到與點B重合時停止,設運動x秒后,Rt△AOB和Rt△CED的重疊部分面積為y,求y與x之間的函數關系式;
(2)當Rt△CED以(1)中的速度和方向運動,運動時間x=2秒時,Rt△CED運動到如圖二所示的位置,若拋物線y= x2+bx+c過點A,G,求拋物線的解析式;
x2+bx+c過點A,G,求拋物線的解析式;
(3)現有一動點P在(2)中的拋物線上運動,試問點P在運動過程中是否存在點P到x軸或y軸的距離為2的情況?若存在,請求出點P的坐標;若不存在,請說明理由.
(1)y=x2(0≤x≤3);(2)y= x2﹣x+3.(3)符合條件的點P有兩個,分別是P1(2,2),P2(﹣2,6).
x2﹣x+3.(3)符合條件的點P有兩個,分別是P1(2,2),P2(﹣2,6).
解析試題分析:(1)根據題意,得重疊部分是等腰直角三角形.根據運動的路程=速度×時間=2x.再根據等腰直角三角形斜邊上的高等于斜邊的一半,即可進一步求得等腰直角三角形的面積;
(2)只需求得點A和點G的坐標.根據等腰直角三角形的兩條直角邊的長即可寫出點A的坐標,根據運動的路程=速度×時間,得到OE=4,再進一步根據等腰直角三角形的性質求得G(2,2),然后根據待定系數法代入求解;
(3)根據題意,應考慮兩種情況.若點P到y軸的距離是2,即點的橫坐標是±2;當點P到x軸的距離是2,即點的縱坐標是±2.
試題解析:(1)①由題意知重疊部分是等腰直角三角形,作GH⊥OE.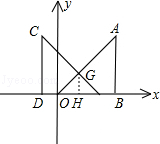
∴OE=2x,GH=x,
∵y= OE•GH=
OE•GH= •2x•x=x2(0≤x≤3)
•2x•x=x2(0≤x≤3)
(2)A(6,6)
當x=2時,OE=2×2=4.
∴OH=2,HG=2,
∴G(2,2).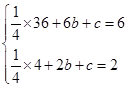
∴解得:
∴y= x2﹣x+3.
x2﹣x+3.
(3)設P(m,n).
當點P到y軸的距離為2時,
有|m|=2,
∴|m|=2.當m=2時,得n=2,
當m=﹣2時,得n=6.
當點P到x軸的距離為2時,有|n|=2.
∵y= x2﹣x+3
x2﹣x+3
= (x﹣2)2+2>0
(x﹣2)2+2>0
∴n=2.當n=2時,得m=2.
綜上所述,符合條件的點P有兩個,分別是P1(2,2),P2(﹣2,6).
考點:二次函數綜合題.


科目:初中數學 來源: 題型:解答題
如圖,排球運動員站在點O處練習發球,將球從點O正上方2米的點A處發出把球看成點,其運行的高度y(米)與運行的水平距離x(米)滿足關系式y=a(x﹣6)2+h,已知 球網與點O的水平距離為9米,高度為2.43米,球場的邊界距點O的水平距離為18米.
(1)當h=2.6時,求y與x的函數關系式.
(2)當h=2.6時,球能否越過球網?球會不會出界?請說明理由.
(3)若球一定能越過球網,又不出邊界.則h的取值范圍是多少?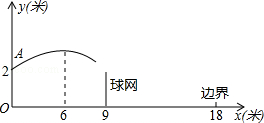
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知二次函數的圖像經過點A(6,0)、B(-2,0)和點C(0,-8)
(1)求該二次函數的解析式;
(2)設該二次函數圖象的頂點為M,若點K為x軸上的動點,當△KCM的周長最小時,求K的坐標;
(3)連接AC,有兩動點P、Q同時從點O出發,其中點P以每秒3個單位長度的速度沿折線按O-A-C的路線運動,點Q以每秒8個單位長度的速度沿折線按O-C-A的路線運動,當P、Q兩點相遇時它們都停止運動,設P、Q同時從點O出發t秒時,△OPQ的面積為S;
①請問P、Q兩點在運動過程中,是否存在PQ∥OC?若存在,請求出此時t的值;若不存在,請說明理由;
② 請求出S關于t的函數關系式,并寫出自變量t的取值范圍;
|


查看答案和解析>>
科目:初中數學 來源: 題型:解答題
“丹棱凍粑”是眉山著名特色小吃,產品暢銷省內外,現有一個產品銷售點在經銷時發現:如果每箱產品盈利10元,每天可售出50箱;若每箱產品漲價1元,日銷售量將減少2箱.
(1)現該銷售點每天盈利600元,同時又要顧客得到實惠,那么每箱產品應漲價多少元?
(2)若該銷售點單純從經濟角度考慮,每箱產品應漲價多少元才能獲利最高?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
某商品現在的售價為每件35元.每天可賣出50件.市場調查反映:如果調整價格.每降價1元,每天可多賣出2件.請你幫助分析,當每件商品降價多少元時,可使每天的銷售額最大,最大銷售額是多少?
設每件商品降價x元.每天的銷售額為y元.
(1)分析:根據問題中的數量關系.用含x的式子填表:
| | 原價 | 每件降價1元 | 每件降價2元 | … | 每件降價x元 |
| 每件售價(元) | 35 | 34 | 33 | … | |
| 每天售量(件) | 50 | 52 | 54 | … | |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜邊BC上的高,垂足為D,BE=1cm.點M從點B出發沿BC方向以1cm/s的速度運動,點N從點E出發,與點M同時同方向以相同的速度運動,以MN為邊在BC的上方作正方形MNGH.點M到達點D時停止運動,點N到達點C時停止運動.設運動時間為t(s).
(1)當t為何值時,點G剛好落在線段AD上?
(2)設正方形MNGH與Rt△ABC重疊部分的圖形的面積為S,當重疊部分的圖形是正方形時,求出S關于t的函數關系式并寫出自變量t的取值范圍.
(3)設正方形MNGH的邊NG所在直線與線段AC交于點P,連接DP,當t為何值時,△CPD是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,Rt△ABO的兩直角邊OA、OB分別在x軸的負半軸和y軸的正半軸上,O為坐標原點,A、B兩點的坐標分別為(-3,0)、(0,4),拋物線y= x2+bx+c經過點B,且頂點在直線x=
x2+bx+c經過點B,且頂點在直線x= 上.
上.
(1)求拋物線對應的函數關系式;
(2)若把△ABO沿x軸向右平移得到△DCE,點A、B、O的對應點分別是D、C、E,當四邊形ABCD是菱形時,試判斷點C和點D是否在該拋物線上,并說明理由;
(3)在(2)的條件下,連接BD,已知對稱軸上存在一點P使得△PBD的周長最小,求出P點的坐標;
(4)在(2)、(3)的條件下,若點M是線段OB上的一個動點(點M與點O、B不重合),過點M作MN∥BD交x軸于點N,連接PM、PN,設OM的長為t,△PMN的面積為S,求S和t的函數關系式,并寫出自變量t的取值范圍,S是否存在最大值?若存在,求出最大值和此時M點的坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com