
如圖,在平面直角坐標系xOy中,拋物線y=ax2+bx+c交y軸于點C(0,4),對稱軸x=2與x軸交于點D,頂點為M,且DM=OC+OD.
(1)求該拋物線的解析式;
(2)設點P(x,y)是第一象限內該拋物線上的一個動點,△PCD的面積為S,求S關于x的函數關系式,并寫出自變量x的取值范圍;
(3)在(2)的條件下,若經過點P的直線PE與y軸交于點E,是否存在以O、P、E為頂點的三角形與△OPD全等?若存在,請求出直線PE的解析式;若不存在,請說明理由.
解:(1)由題意得:OC=4,OD=2,∴DM=OC+OD=6。
∴頂點M坐標為(2,6)。
設拋物線解析式為:y=a(x﹣2)2+6,
∵點C(0,4)在拋物線上,∴4=4a+6,解得a=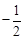 。
。
∴拋物線的解析式為:y=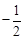 (x﹣2)2+6=
(x﹣2)2+6=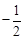 x2+2x+4。
x2+2x+4。
(2)如答圖1,過點P作PE⊥x軸于點E.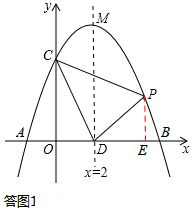
∵P(x,y),且點P在第一象限,∴PE=y,OE=x。
∴DE=OE﹣OD=x﹣2.
∴S=S梯形PEOC﹣S△COD﹣S△PDE= (4+y)•x﹣
(4+y)•x﹣ ×2×4﹣
×2×4﹣ (x﹣2)•y=y+2x﹣4。
(x﹣2)•y=y+2x﹣4。
將y=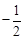 x2+2x+4代入上式得:S=
x2+2x+4代入上式得:S=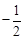 x2+2x+4+2x﹣4=
x2+2x+4+2x﹣4=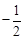 x2+4x。
x2+4x。
在拋物線解析式y=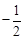 x2+2x+4中,令y=0,即
x2+2x+4中,令y=0,即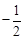 x2+2x+4=0,解得x=2±
x2+2x+4=0,解得x=2±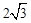 .
.
設拋物線與x軸交于點A、B,則B(2+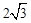 ,0)。
,0)。
∴0<x<2+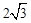 .
.
∴S關于x的函數關系式為:S=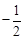 x2+4x(0<x<2+
x2+4x(0<x<2+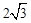 )。
)。
(3)存在。若以O、P、E為頂點的三角形與△OPD全等,可能有以下情形:
①OD=OP。
由圖象可知,OP最小值為4,即OP≠OD,故此種情形不存在。
②OD=OE。
若點E在y軸正半軸上,如答圖2所示,此時△OPD≌△OPE。
∴∠OPD=∠OPE,即點P在第一象限的角平分線上。
∴直線PE的解析式為:y=x。
若點E在y軸負半軸上,易知此種情形下,兩個三角形不可能全等,故不存在。
③OD=PE。
∵OD=2,∴第一象限內對稱軸右側的點到y軸的距離均大于2。
∴點P只能位于對稱軸左側或與頂點M重合。
若點P位于第一象限內拋物線對稱軸的左側,易知△OPE為鈍角三角形,而△OPD為銳角三角形,則不可能全等。
若點P與點M重合,如答圖3所示,此時△OPD≌OPE,四邊形PDOE為矩形。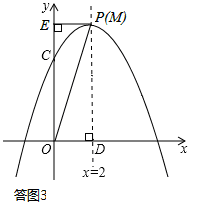
∴直線PE的解析式為:y=6。
綜上所述,存在以O、P、E為頂點的三角形與△OPD全等,直線PE的解析式為y=x或y=6。
解析試題分析:(1)首先求出點M的坐標,然后利用頂點式和待定系數法求出拋物線的解析式。
(2)如答圖1所示,作輔助線構造梯形,利用S=S梯形PEOC﹣S△COD﹣S△PDE求出S關于x的表達式;求出拋物線與x軸正半軸的交點坐標,得到自變量的取值范圍。
(3)由于三角形的各邊,只有OD=2是確定長度的,因此可以以OD為基準進行分類討論:
①OD=OP,因為第一象限內點P到原點的距離均大于4,因此OP≠OD,此種情形排除。
②OD=OE.分析可知,只有如答圖2所示的情形成立。
③OD=PE.分析可知,只有如答圖3所示的情形成立。


科目:初中數學 來源: 題型:解答題
如圖,已知拋物線y=ax2+bx+3與x軸交于A、B兩點,過點A的直線l與拋物線交于點C,其中A點的坐標是(1,0),C點坐標是(4,3).
(1)求拋物線的解析式;
(2)在(1)中拋物線的對稱軸上是否存在點D,使△BCD的周長最小?若存在,求出點D的坐標,若不存在,請說明理由;
(3)若點E是(1)中拋物線上的一個動點,且位于直線AC的下方,試求△ACE的最大面積及E點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
某商場經營某種品牌的玩具,購進時的單價是30元,根據市場調查:在一段時間內,銷售單價是40元時,銷售量是600件,而銷售單價每漲1元,就會少售出10件玩具.
(1)不妨設該種品牌玩具的銷售單價為x元(x>40),請你分別用x的代數式來表示銷售量y件和銷售該品牌玩具獲得利潤w元,并把結果填寫在表格中:
| 銷售單價(元) | x |
| 銷售量y(件) | |
| 銷售玩具獲得利潤w(元) | |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,四邊形ABCD是菱形,對角線AC與BD交于點O,且AC=80,BD=60.動點M、N分別以每秒1個單位的速度從點A、D同時出發,分別沿A→O→D和D→A運動,當點N到達點A時,M、N同時停止運動.設運動時間為t秒.
(1)求菱形ABCD的周長;
(2)記△DMN的面積為S,求S關于t的解析式,并求S的最大值;
(3)當t=30秒時,在線段OD的垂直平分線上是否存在點P,使得∠DPO=∠DON?若存在,這樣的點P有幾個?并求出點P到線段OD的距離;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平面直角坐標系中,O為坐標原點,拋物線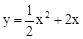 與x軸相交于O、B,頂點為A,連接OA.
與x軸相交于O、B,頂點為A,連接OA.
(1)求點A的坐標和∠AOB的度數;
(2)若將拋物線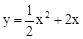 向右平移4個單位,再向下平移2個單位,得到拋物線m,其頂點為點C.連接OC和AC,把△AOC沿OA翻折得到四邊形ACOC′.試判斷其形狀,并說明理由;
向右平移4個單位,再向下平移2個單位,得到拋物線m,其頂點為點C.連接OC和AC,把△AOC沿OA翻折得到四邊形ACOC′.試判斷其形狀,并說明理由;
(3)在(2)的情況下,判斷點C′是否在拋物線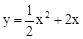 上,請說明理由;
上,請說明理由;
(4)若點P為x軸上的一個動點,試探究在拋物線m上是否存在點Q,使以點O、P、C、Q為頂點的四邊形是平行四邊形,且OC為該四邊形的一條邊?若存在,請直接寫出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平面直角坐標系中,拋物線y=ax2+bx﹣2 與x軸交于點A(﹣1,0)、B(4,0).點M、N在x軸上,點N在點M右側,MN=2.以MN為直角邊向上作等腰直角三角形CMN,∠CMN=90°.設點M的橫坐標為m.
(1)求這條拋物線所對應的函數關系式.
(2)求點C在這條拋物線上時m的值.
(3)將線段CN繞點N逆時針旋轉90°后,得到對應線段DN.
①當點D在這條拋物線的對稱軸上時,求點D的坐標.
②以DN為直角邊作等腰直角三角形DNE,當點E在這條拋物線的對稱軸上時,直接寫出所有符合條件的m值.
(參考公式:拋物線y=ax2+bx+c(a≠0)的頂點坐標為 )
)
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,平面直角坐標系中,以點C(2, )為圓心,以2為半徑的圓與x軸交于A,B兩點.
)為圓心,以2為半徑的圓與x軸交于A,B兩點.
(1)求A,B兩點的坐標;
(2)若二次函數y=x2+bx+c的圖象經過點A,B,試確定此二次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
2011年11月28日至12月9日,聯合國氣候變化框架公約第17次締約方會議在南非德班召開,大會通過了“德班一攬子決議”(DurbanPackageOutcome),建立德班增強行動平臺特設工作組,決定實施《京都議定書》第二承諾期并啟動綠色氣候基金,中國的積極態度贏得與會各國的尊重.
在氣候對人類生存壓力日趨加大的今天,發展低碳經濟,全面實現低碳生活逐漸成為人們的共識.某企業采用技術革新,節能減排.從去年1至6月,該企業二氧化碳排放量y1(噸)與月份x(1≤x≤6,且x取整數)之間的函數關系如下表:
| 月份x(月) | 1 | 2 | 3 | 4 | 5 | 6 |
| 二氧化碳排放量y1(噸) | 600 | 300 | 200 | 150 | 120 | 100 |
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
點(﹣1,y1),(2,y2),(3,y3)均在函數y= 的圖象上,則y1,y2,y3的大小關系是( )
的圖象上,則y1,y2,y3的大小關系是( )
| A.y3<y2<y1 | B.y2<y3<y1 |
| C.y1<y2<y3 | D.y1<y3<y2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com