
已知拋物線y= x2+bx+c過點(-6,-2),與y軸交于點C,且對稱軸與x軸交于點B(-2,0),頂點為A.
x2+bx+c過點(-6,-2),與y軸交于點C,且對稱軸與x軸交于點B(-2,0),頂點為A.
(1)求該拋物線的解析式和A點坐標;
(2)若點D是該拋物線上的一個動點,且使△DBC是以B為直角頂點BC為腰的等腰直角三角形,求點D坐標;
(3)若點M是第二象限內該拋物線上的一個動點,經過點M的直線MN與y軸交于點N,是否存在以O、M、N為頂點的三角形與△OMB全等?若存在,請求出直線MN的解析式;若不存在,請說明理由.
(1)A點的坐標為(﹣2,6);
(2)D點的坐標為:(2,﹣2);
(3)存在.直線MN的解析式為y=6或y=﹣ x+2.
x+2.
解析試題分析:(1)首先依據頂點坐標先求出b的值,然后利用待定系數法求出拋物線的解析式;
(2)過B點作CB的垂線交拋物線與D,然后過D點作x軸的垂線,垂足為E,通過三角形全等即可求得點D的坐標.
(3)由于三角形的各邊,只有OB=2是確定長度的,因此可以以OB為基準進行分類討論:
①OB=OM.因為第二象限內點P到原點的距離均大于4,因此OB≠OM,此種情形排除;
②OB=ON.分析可知,只有如答圖2所示的情形成立;
③OB=MN.分析可知,只有如答圖3所示的情形成立.
試題解析:(1)∵對稱軸與x軸交于點B(﹣2,0),
∴A的橫坐標為:x=﹣2,
∴﹣ =﹣2,
=﹣2,
解得;b=﹣2,
∴拋物線為y=﹣ x2﹣2x+c,
x2﹣2x+c,
∵拋物線y=﹣ x2+bx+c過點(﹣6,﹣2),
x2+bx+c過點(﹣6,﹣2),
∴代入得﹣2=﹣ ×(﹣6)2﹣2×(﹣6)+c,解得c=4,
×(﹣6)2﹣2×(﹣6)+c,解得c=4,
∴該拋物線的解析式為:y=﹣ x2﹣2x+4,
x2﹣2x+4,
∴y=﹣ x2﹣2x+4=﹣
x2﹣2x+4=﹣ (x2+4x+4)+6)=﹣
(x2+4x+4)+6)=﹣ (x+2)2+6
(x+2)2+6
∴A點的坐標為(﹣2,6);
(2)過B點作CB的垂線交拋物線與D,然后過D點作x軸的垂線,垂足為E,
∵∠CBD=90°,
∴∠CBO+∠EBD=90°,
∵∠BCO+∠CBO+90°,
∴∠EBD=∠BCO,∠CBO=∠BDE,
∴在△CBO與△BDE中
∴△CBO≌△BDE(ASA)
∴DE=OB=2,BE=OC=4
∴D點的坐標為(2,﹣2)或(﹣6.2),
把(2,﹣2)或(﹣6.2)分別代入y=﹣ x2﹣2x+4,(﹣2,2)合適,(﹣6,2)不合適,
x2﹣2x+4,(﹣2,2)合適,(﹣6,2)不合適,
∴D點的坐標為:(2,﹣2)
圖1
(3)存在.
若以O、M、N為頂點的三角形與△OBM全等,可能有以下情形:
(I)OB=OM.
由圖象可知,OM最小值為4,即OM≠OB,故此種情形不存在.
(II)OB=ON.
若點M在y軸正半軸上,如答圖2所示: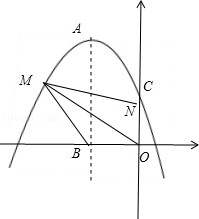
圖2
此時△OBM≌△OMN,
∴∠OMB=∠OMN,即點P在第二象限的角平分線上,ON=OB=2,M點坐標為:(4,4),
∴直線PE的解析式為:y=﹣ x+2;
x+2;
若點E在y軸負半軸上,易知此種情形下,兩個三角形不可能全等,故不存在.
(III)OB=MN.
∵OB=2,
∴第二象限內對稱軸左側的點到y軸的距離均大于2,
則點M只能位于對稱軸右側或與頂點A重合.
若點M位于第二象限內拋物線對稱軸的右側,易知△OMN為鈍角三角形,而△OMB為銳角三角形,則不可能全等;
若點M與點A重合,如答圖3所示,此時△OBM≌△OMN,四邊形MNOB為矩形,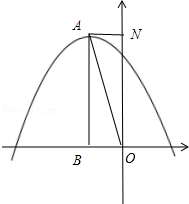
圖3
∴直線MN的解析式為:y=6.
綜上所述,存在以O、M、N為頂點的三角形與△OMB全等,直線MN的解析式為y=6,y=﹣ x+2.
x+2.
考點:二次函數綜合題.


 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:初中數學 來源: 題型:解答題
某種上屏每天的銷售利潤y(元)與銷售單價x(元)之間滿足關系:y=ax2+bx﹣75.其圖象如圖.
(1)銷售單價為多少元時,該種商品每天的銷售利潤最大?最大利潤為多少元?
(2)銷售單價在什么范圍時,該種商品每天的銷售利潤不低于16元?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知拋物線y=ax2+x+c(a≠0)經過A(﹣1,0),B(2,0)兩點,與y軸相交于點C,該拋物線的頂點為點M,對稱軸與BC相交于點N,與x軸交于點D.
(1)求該拋物線的解析式及點M的坐標;
(2)連接ON,AC,證明:∠NOB=∠ACB;
(3)點E是該拋物線上一動點,且位于第一象限,當點E到直線BC的距離為 時,求點E的坐標;
時,求點E的坐標;
(4)在滿足(3)的條件下,連接EN,并延長EN交y軸于點F,E、F兩點關于直線BC對稱嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知拋物線 與x軸交點為A、B(點B在點A的右側),與y軸交于點C.
與x軸交點為A、B(點B在點A的右側),與y軸交于點C.
(1)試用含m的代數式表示A、B兩點的坐標;
(2)當點B在原點的右側,點C在原點的下方時,若 是等腰三角形,求拋物線的解析式;
是等腰三角形,求拋物線的解析式;
(3)已知一次函數 ,點P(n,0)是x軸上一個動點,在(2)的條件下,過點P作垂直于x軸的直線交這個一次函數的圖象于點M,交拋物線
,點P(n,0)是x軸上一個動點,在(2)的條件下,過點P作垂直于x軸的直線交這個一次函數的圖象于點M,交拋物線 于點N,若只有當
于點N,若只有當 時,點M位于點N的下方,求這個一次函數的解析式.
時,點M位于點N的下方,求這個一次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線y=ax2 + bx + c 交x軸于A、B兩點,交y軸于點C,對稱軸為直線x=1,已知:A(-1,0)、C(0,-3)。
(1)求拋物線y= ax2 + bx + c 的解析式;
(2)求△AOC和△BOC的面積比;
(3)在對稱軸上是否存在一個P點,使△PAC的周長最小。若存在,請你求出點P的坐標;若不存在,請你說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在△ABC中,∠BAC=90°, BC∥x軸,拋物線y=ax2-2ax+3經過△ABC的三個頂點,并且與x軸交于點D、E,點A為拋物線的頂點.
(1)求拋物線的解析式;
(2)連接CD,在拋物線的對稱軸上是否存在一點P使△PCD為直角三角形,若存在,求出所有符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知拋物線 與x軸交于點
與x軸交于點 、C,與y軸交于點B(0,3),拋物線的頂點為p。
、C,與y軸交于點B(0,3),拋物線的頂點為p。
(1)求拋物線的解析式;
(2)若拋物線向下平移k個單位后經過點(-5,6)。
①求k的值及平移后拋物線所對應函數的最小值;
②設平移后拋物線與y軸交于點D,頂點為Q,點M是平移后的拋物線上的一個動點。請探究:當點M在何處時,△MBD的而積是△MPQ面積的2倍?求出此時點M的坐標。
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知拋物線 與x軸的交點為A、D(A在D的右側),與y軸的交點為C.
與x軸的交點為A、D(A在D的右側),與y軸的交點為C.
(1)直接寫出A、D、C三點的坐標;
(2)在拋物線的對稱軸上找一點M,使得MD+MC的值最小,并求出點M的坐標;
(3)設點C關于拋物線對稱的對稱點為B,在拋物線上是否存在點P,使得以A、B、C、P四點為頂點的四邊形為梯形?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
平面直角坐標系中,拋物線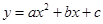 交
交 軸于A、B兩點(點A在點B左側),與
軸于A、B兩點(點A在點B左側),與 軸交于點C,點A、C的坐標分別為(-3,0),(0,3),對稱軸直線
軸交于點C,點A、C的坐標分別為(-3,0),(0,3),對稱軸直線 交
交 軸于點E,點D為頂點.
軸于點E,點D為頂點.
(1)求拋物線的解析式;
(2)點P是直線AC下方的拋物線上一點,且 ,,求點P的坐標;
,,求點P的坐標;
(3)點M是第一象限內拋物線上一點,且∠MAC=∠ADE,求點M的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com