
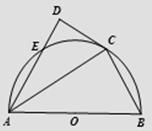
已知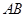 為半圓
為半圓 的直徑,
的直徑,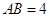 ,
, 為半圓上一點,過點
為半圓上一點,過點 作半圓的切線
作半圓的切線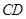 ,過點
,過點 作
作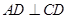 于
于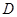 ,交圓于點
,交圓于點 ,
,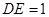 .
.
(Ⅰ)求證: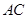 平分
平分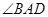 ;
;
(Ⅱ)求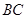 的長.
的長.
(1)證明過程詳見解析;(2)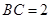 .
.
解析試題分析:本題主要以圓為幾何背景考查線線平行、線線垂直的證明,證明角之間的相等關系以及四點共圓的證明及性質的應用,考查學生的轉化能力與化歸能力和推理論證能力.第一問,利用圓中的半徑長都相等得出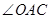 和
和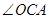 相等,而
相等,而 為圓的切線,所以
為圓的切線,所以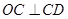 ,所以會得出
,所以會得出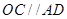 ,所以
,所以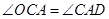 ,最終得出
,最終得出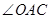 與
與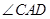 相等,所以得出
相等,所以得出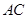 平分
平分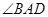 ;第二問,利用第一問的結論,得出
;第二問,利用第一問的結論,得出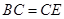 ,而
,而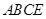 共圓,可得到
共圓,可得到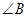 與
與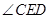 相等,所以在
相等,所以在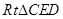 與
與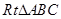 中,分別求出
中,分別求出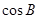 與
與 ,求出
,求出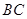 的長.
的長.
試題解析:(Ⅰ)連結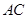 ,因為
,因為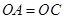 ,所以
,所以 ,2分
,2分
因為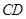 為半圓的切線,所以
為半圓的切線,所以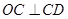 ,又因為
,又因為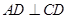 ,所以
,所以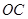 ∥
∥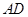 ,
,
所以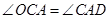 ,
,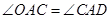 ,所以
,所以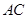 平分
平分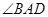 .4分
.4分
(Ⅱ)由(Ⅰ)知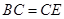 ,6分
,6分
連結 ,因為
,因為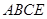 四點共圓,
四點共圓,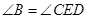 ,所以
,所以 ,8分
,8分
所以 ,所以
,所以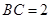 .10分
.10分
考點:1.內錯角相等;2.四點共圓;3.直角三角形中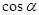 的計算.
的計算.


科目:高中數學 來源: 題型:解答題
如圖,圓O的半徑OC垂直于直徑AB,弦CD交半徑 OA于E,過D的切線與BA的延長線交于M.
(1)求證:MD=ME;
(2)設圓O的半徑為1,MD= ,求MA及CE的長.
,求MA及CE的長.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,AB為⊙O的直徑,直線CD與⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,連接AE,BE.證明: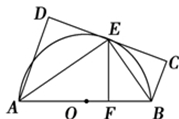
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,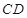 為△
為△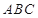 外接圓的切線,
外接圓的切線,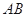 的延長線交直線
的延長線交直線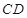 于點
于點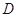 ,
,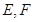 分別為弦
分別為弦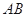 與弦
與弦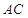 上的點,且
上的點,且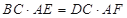 ,
,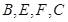 四點共圓.
四點共圓. 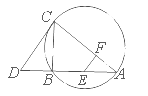
(Ⅰ)證明: 是△
是△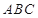 外接圓的直徑;
外接圓的直徑;
(Ⅱ)若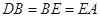 ,求過
,求過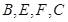 四點的圓的面積與△
四點的圓的面積與△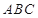 外接圓面積的比值.
外接圓面積的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,AB是圓O的直徑,C,D是圓O上兩點,AC與BD相交于點E,GC,GD是圓O的切線,點F在DG的延長線上,且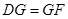 。求證:
。求證:
(Ⅰ)D、E、C、F四點共圓; (Ⅱ)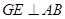

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,圓O的直徑AB=4,C為圓周上一點,BC=2,過C作圓O的切線l,過A作l的垂線AD,AD分別與直線l、圓O交于點D,E,求線段AE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com