
國家助學貸款是由財政貼息的信用貸款,旨在幫助高校家庭經濟困難學生支付在校期間所需的學費、住宿費及生活費。每一年度申請總額不超過6000元。某大學2012屆畢業生凌霄在本科期間共申請了24000元助學貸款,并承諾畢業后3年(按36個月計)內還清。簽約單位提供的工資標準為第一年內每月1500元,第13個月開始每月工資比前一個月增加5%直到4000元。凌霄同學計劃前12個月每月還款500元,第13個月開始每月還款比前一個月多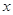 元.
元.
(1)若凌霄同學恰好在第36個月(即畢業后3年)還清貸款,求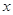 值;(6分)
值;(6分)
(2)當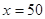 時,凌霄同學將在畢業后第幾個月還清最后一筆貸款?他當月工資余額能否滿足當月3000元的基本生活費?(6分)
時,凌霄同學將在畢業后第幾個月還清最后一筆貸款?他當月工資余額能否滿足當月3000元的基本生活費?(6分)
(參考數據: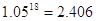 ,
,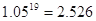 ,
,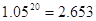 ,
, 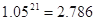 )
)
科目:高中數學 來源: 題型:解答題
已知函數 .
.
(1)若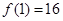 ,函數
,函數 是R上的奇函數,當
是R上的奇函數,當 時
時 ,
,
(i)求實數 與
與 的值;
的值;
(ii)當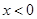 時,求
時,求 的解析式;
的解析式;
(2)若方程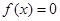 的兩根中,一根屬于區間
的兩根中,一根屬于區間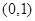 ,另一根屬于區間
,另一根屬于區間 ,求實數
,求實數 的
的
取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
二次函數 的圖像頂點為
的圖像頂點為 ,且圖像在x軸上截得線段長為8
,且圖像在x軸上截得線段長為8
(1)求函數 的解析式;
的解析式;
(2)令
①若函數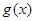 在
在 上是單調增函數,求實數
上是單調增函數,求實數 的取值范圍;
的取值范圍;
②求函數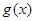 在
在 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
將邊長為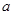 的一塊正方形鐵皮的四角各截去一個大小相同的小正方形,然后將四邊折起做成一個無蓋的方盒.欲使所得的方盒有最大容積,截去的小正方形的邊長應為多少?方盒的最大容積為多少?
的一塊正方形鐵皮的四角各截去一個大小相同的小正方形,然后將四邊折起做成一個無蓋的方盒.欲使所得的方盒有最大容積,截去的小正方形的邊長應為多少?方盒的最大容積為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數 的最小值為1,且
的最小值為1,且 .
.
(1)求 的解析式;
的解析式;
(2)若 在區間
在區間 上不單調,求實數
上不單調,求實數 的取值范圍;
的取值范圍;
(3)在區間 上,
上,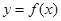 的圖像恒在
的圖像恒在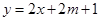 的圖像上方,試確定實數
的圖像上方,試確定實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了在夏季降溫和冬季供暖時減少能源損耗,房屋的屋頂和外墻需要建造隔熱層。某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元。該建筑物每年的能源消耗費用C(單位:萬元)與隔熱層厚度x(單位:cm)滿足關系:C(x)= 若不建隔熱層(即x=0時),每年能源消耗費用為8萬元.設f(x)為隔熱層建造費用與20年的能源消耗費用之和.
若不建隔熱層(即x=0時),每年能源消耗費用為8萬元.設f(x)為隔熱層建造費用與20年的能源消耗費用之和.
(1)求k的值;
(2)求f(x)的表達式;
(3)利用“函數 (其中
(其中 為大于0的常數),在
為大于0的常數),在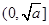 上是減函數,在
上是減函數,在 上是增函數”這一性質,求隔熱層修建多厚時,總費用f(x)達到最小,并求出這個最小值.
上是增函數”這一性質,求隔熱層修建多厚時,總費用f(x)達到最小,并求出這個最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
水庫的蓄水量隨時間而變化,現用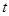 表示時間,以月為單位,年初為起點,根據歷年數據,某水庫的蓄水量(單位:億立方米)關于
表示時間,以月為單位,年初為起點,根據歷年數據,某水庫的蓄水量(單位:億立方米)關于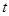 的近似函數關系式為:
的近似函數關系式為: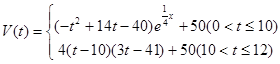
(1)該水庫的蓄水量小于50的時期稱為枯水期,以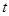 表示第
表示第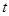 月份(
月份(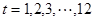 ),問:同一年內哪些月份是枯水期?
),問:同一年內哪些月份是枯水期?
(2)求一年內哪個月份該水庫的蓄水量最大,并求最大蓄水量。(取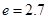 計算)
計算)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com