.(本小題滿分12分)
已知函數(shù)

.
(Ⅰ)求函數(shù)

的最大值,并寫出

取最大值時

的取值集合;
(Ⅱ)已知

中,角

的對邊分別為

若

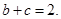
求實數(shù)

的最小值.
(Ⅰ)

. (Ⅱ)當(dāng)

時,實數(shù)

取最小值1。
(1)利用三角函數(shù)公式把

化為

的形式,由正弦函數(shù)的性質(zhì)求出其最值和對應(yīng)的

的值;(2)由(1)結(jié)合三角形中角的范圍求出

,再由余弦定理表示出

,利用不等式求出其最值.
(Ⅰ)


.
∴函數(shù)

的最大值為

.
要使

取最大值,則
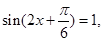

,解得

.
故

的取值集合為

. ……………………………………………(6分)
(Ⅱ)由題意,

,化簡得


,

, ∴

, ∴

在

中,根據(jù)余弦定理,得

.
由

,知

,即
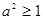
.
∴當(dāng)

時,實數(shù)

取最小值

………………………………………………(12分)
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
將

的圖象向左平移

個單位,所得圖象的函數(shù)解析式為 ( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(滿分10分)函數(shù)

在一個周期內(nèi)的圖象如圖,求函數(shù)的解析式

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
函數(shù)

在

上的遞增區(qū)間為
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知函數(shù)

的最大值為3,

的圖像與

軸的交點坐標為

,其相鄰兩條對稱軸間的距離為

,則


____________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
函數(shù)y=cos( -x)是( )
| A.[-π ,0 ]上的增函數(shù) | B.[-, ]上的增函數(shù) |
| C.[-, ]上的增函數(shù) | D.[ , ]上的增函數(shù) |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
下列函數(shù)中,最小正周期為
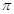
且在
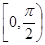
單調(diào)遞增的是
查看答案和解析>>

 .
. 的最大值,并寫出
的最大值,并寫出 取最大值時
取最大值時 的取值集合;
的取值集合; 中,角
中,角 的對邊分別為
的對邊分別為 若
若
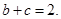 求實數(shù)
求實數(shù) 的最小值.
的最小值.