
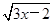 ;
;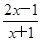 ,x∈[3,5];
,x∈[3,5];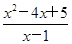 (x>1).
(x>1).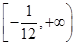 (2)[-4,5].(3)
(2)[-4,5].(3)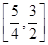 (4)[2
(4)[2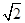 -2,+∞).
-2,+∞).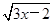 =t,t≥0,則y=
=t,t≥0,則y=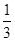 (t2+2)-t=
(t2+2)-t=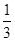
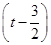 2-
2-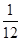 ,當t=
,當t=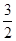 時,y有最小值-
時,y有最小值-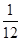 ,故所求函數的值域為
,故所求函數的值域為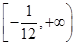 .
.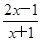 =2-
=2-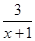 ,結合圖象知,函數在[3,5]上是增函數,所以ymax=
,結合圖象知,函數在[3,5]上是增函數,所以ymax=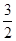 ,ymin=
,ymin=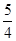 ,故所求函數的值域是
,故所求函數的值域是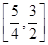 .
.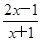 ,得x=
,得x=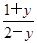 .因為x∈[3,5],所以3≤
.因為x∈[3,5],所以3≤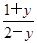 ≤5,解得
≤5,解得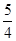 ≤y≤
≤y≤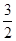 ,
,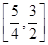 .
.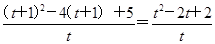 =t+
=t+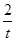 -2(t>0).
-2(t>0).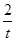 ≥2
≥2 =2
=2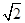 ,當且僅當t=
,當且僅當t=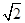 ,即x=
,即x=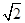 +1時,等號成立,
+1時,等號成立,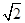 -2,+∞).
-2,+∞).

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com