中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

已知函數f（x）＝sinωx＋cosωx（ω＞0）的最小正周期為4π，則對該函數的圖象與性質判斷錯誤的是

A．關于點（－，0）對稱           B．在（0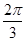，）上遞增

C．關于直線x＝對稱             D．在（－，0）上遞增

 

【答案】

C

【解析】由f（x）＝sinωx＋cosωx，最小正周期為4π，得。

當，所以圖象關于直線x＝對稱錯誤

 

練習冊系列答案
相關習題

科目：高中數學 來源：張家港市后塍高級中學2006~2007年第一學期高三數學十二月調研測試卷 題型：044

已知函數f(x)＝ax2＋bx＋1(a，b∈R)

(1)

若f(－1)＝0，且對任意實數x均有f(x)≥0成立，求f(x)表達式

(2)

在1條件下，當x∈[－2，2]時，S(x)＝xf(x)－kx單調遞增，求實數k取值范圍.

查看答案和解析>>

科目：高中數學 來源：山東省鄆城一中2012屆高三上學期寒假作業數學試卷(12) 題型：013

已知函數f(x)＝x3＋ax2＋bx＋c，在定義域x∈[－2，2]上表示的曲線過原點，且在x＝±1處的切線斜率均為－1．有以下命題：

①f(x)是奇函數；②若f(x)在[s，t]內遞減，則|t－s|的最大值為4；③f(x)的最大值為M，最小值為m，則M＋m＝0；④若對x∈[－2，2]，k≤恒成立，則k的最大值為2．其中正確命題的個數為

[　　]

A．1個

B．2個

C．3個

D．4個

查看答案和解析>>

科目：高中數學 來源：浙江省瑞安中學2012屆高三10月月考數學文科試題 題型：044

已知函數，g(x)＝lnx．

(1)設F(x)＝f(x)＋g(x)，當a＝2時，求F(x)在上的單調區間；

(2)在條件(1)下，若對任意(e為自然對數的底數)均有|F(x1)－F(x2)|＜3m＋－6恒成立，求實數m的取值范圍；

(3)設G(x)＝f(x)－g(x)在x＝1處的切線與坐標軸圍成的三角形面積為S，存在α∈N*且a≠4使得t≤S成立，求最大的整數t的值．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知函數f(x)＝ax3＋x2在x＝－1處取得極值，記g(x)＝，程序框圖如圖所示，若輸出的結果S>，則判斷框中可以填入的關于n的判斷條件是                                   (　　)

A．n≤2 011?                       B．n≤2 012?

C．n>2 011?                        D．n>2 012?

查看答案和解析>>

科目：高中數學 來源：2013-2014學年江西贛州四所重點中學高三上學期期末聯考理數學試卷（解析版） 題型：選擇題

已知函數f(x)＝ax3＋x2在x＝－1處取得極大值，記g(x)＝。程序框圖如圖所示，若輸出的結果S＝，則判斷框中可以填入的關于n的判斷條件是（    ）

A．n≤2013   B．n≤2014        C．n＞2013     D．n＞2014

 

查看答案和解析>>

同步練習冊答案