
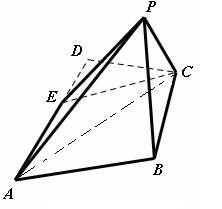
��Dһ����ABC���������Σ���ABD�ǵ���ֱ�������Σ�AB=BD=2������ABD��߅AB���� ʹ�á�ABD�c��ABC��ֱ����� ,��D�����ڶ����
,��D�����ڶ���� ��.
��.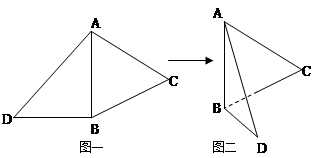
(1)���C��BD��AC��
(2)��D��C֮�g�ľ��x��
(3)��DC�c��ABD�ɵĽǵ�����ֵ��
(1)����(j��)���洹ֱ�����|(zh��)������õ�������ֱ���C�����P(gu��n)�I��һ����������ABD ��ABC���õ�
��ABC���õ� BD
BD ��ABC�������C����
��ABC�������C����
(2) 2 (3)
(3)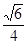
����ԇ�}������ �⣺(1)���}�⣬��ABD ��ABC��AB�ǽ�����
��ABC��AB�ǽ�����
��BD AB��
AB�� BD
BD ��ABC����AC
��ABC����AC ��ABC��
��ABC�� BD��AC�� 4��
BD��AC�� 4��
(2)��(1)֪��BD��ABC����BC ��ABC��
��ABC�� BD��BC��Rt
BD��BC��Rt DBC��BC=BA=2��BD=2��
DBC��BC=BA=2��BD=2�� DC=
DC=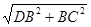 =
=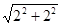 =2
=2 �� 8��
�� 8��
(3)ȡAB�����c(di��n)H���BCH��DH��DC��
 ��ABC����������
��ABC���������� CH
CH AB����
AB���� ��ABC
��ABC ��ABD��
��ABD�� CH
CH ��ABD��
��ABD�� DH��DC����ABD��(n��i)����Ӱ��
DH��DC����ABD��(n��i)����Ӱ��
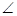 CDH��DC�c��ABD�ɵĽǡ�
CDH��DC�c��ABD�ɵĽǡ�
��CH=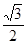 BC=
BC= ����(2)DC=2
����(2)DC=2 ��
�� sin
sin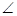 CDH=
CDH=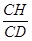 =
=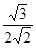 =
=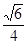 �������� 12��
�������� 12��
���c(di��n)�����g���c(di��n)�����λ���P(gu��n)ϵ
�c(di��n)�u(p��ng)����Qԓԇ�}���P(gu��n)�I���쾚���\(y��n)���ж����������|(zh��)�����õ���ֱ���C�����Լ��ǵ���⣬���ڻ��A(ch��)�}��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D1����Rt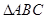 ��
��  ��
�� ��D��E�քe��
��D��E�քe�� �ϵ��c(di��n)����
�ϵ��c(di��n)����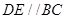 ����
���� ��
�� ����
���� ��λ�ã�ʹ
��λ�ã�ʹ ����D2��
����D2��
�������C��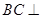 ƽ��
ƽ��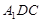 ��
��
������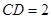 ����
���� �cƽ��
�cƽ��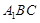 ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D������߅��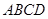 �У�
��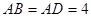 ��
��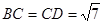 ���c(di��n)
���c(di��n)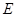 �龀��
�龀�� �ϵ�һ�c(di��n).�F(xi��n)��
�ϵ�һ�c(di��n).�F(xi��n)��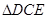 �ؾ���
�ؾ���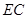 ���۵�
���۵�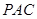 ���c(di��n)
���c(di��n) �c�c(di��n)
�c�c(di��n)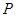 �غϣ���ʹ��ƽ��
�غϣ���ʹ��ƽ��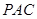
 ƽ��
ƽ��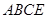 ���B��
���B��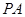 ��
��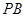 .
.
(��)�C����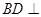 ƽ��
ƽ��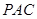 ��
��
(��)�� �����c(di��n)
�����c(di��n) �龀��
�龀�� �����c(di��n)��������
�����c(di��n)�������� �Ĵ�С.
�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�����FS��ABC�ĵ������������Σ�A�c(di��n)�ڂ�(c��)��SBC�ϵ���ӰH�ǡ�SBC�Ĵ���.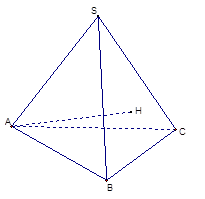
(1)���C��BC��SA
(2)��S�ڵ���ABC��(n��i)����Ӱ��O���C����O������ABC�����ģ�
(3)�������H��AB��C��ƽ��ǵ���30�㣬SA=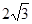 ���������FS��ABC���w�e.
���������FS��ABC���w�e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����D��ʾ�Ķ����wABCDE�У�AB��ƽ��ACD��DE��ƽ��ACD��AC=AD=CD=DE=2��AB=1��G��AD���c(di��n)��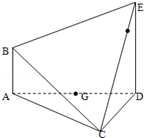
��1��Ո(q��ng)?ji��n)ھ���CE���ҵ��c(di��n)F��λ�ã�ʹ��ǡ��ֱ��BF��ƽ��ACD�����C���@һ��(sh��)��
��2����ƽ��BCE�cƽ��ACD�����J����ǵĴ�С��
��3�����c(di��n)G��ƽ��BCE�ľ��x��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D1����O��ֱ��AB=4���c(di��n)C��D���O�σ��c(di��n)���ҡ�CAB=45o��F(xi��n)��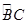 �����c(di��n)����ֱ��AB����ʹ�ɂ�(g��)��A����ƽ�滥�ഹֱ����D2����
�����c(di��n)����ֱ��AB����ʹ�ɂ�(g��)��A����ƽ�滥�ഹֱ����D2����
�������C��OF//ƽ��ACD��
������ ���Ƿ�����c(di��n)
���Ƿ�����c(di��n) ��ʹ��ƽ��
��ʹ��ƽ�� ƽ��ACD?�����ڣ�ԇָ���c(di��n)
ƽ��ACD?�����ڣ�ԇָ���c(di��n) ��λ�ã��������ڣ�Ո(q��ng)�f�����ɣ�
��λ�ã��������ڣ�Ո(q��ng)�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D����ֱ������ABC��A1B1C1�У���BAC��90�㣬AB=AC=2��AA1=6���c(di��n)E��F�քe����BB1��CC1�ϣ���BE��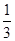 BB1��C1F��
BB1��C1F��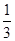 CC1.
CC1.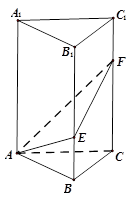
��1������ֱ��AE�cA1 F���ɽǵĴ�С��
��2����ƽ��AEF�cƽ��ABC���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪ABCD�Ǿ��Σ�AD=2AB��E��F(xi��n)�քe�Ǿ���AB��BC�����c(di��n)��PA��ƽ��ABCD.
(��)���C��DF��ƽ��PAF��
(��)����PA����һ�c(di��n)G��ʹEG��ƽ��PFD����(d��ng)PA=AB=4�r(sh��)���������wE-GFD���w�e.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����С�}�M��12�֣���֪�����F ��
�� ƽ��
ƽ��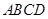 ��
��
��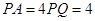 �������ֱ�����Σ�
�������ֱ�����Σ�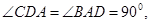
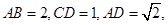
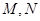 �քe��
�քe��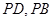 �����c(di��n)��
�����c(di��n)��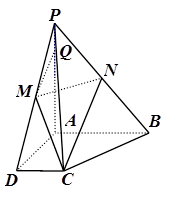
��1�����C��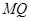 // ƽ��
// ƽ��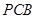 ��
��
��2�������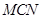 �c����
�c����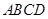 ���ɶ���ǵĴ�С��
���ɶ���ǵĴ�С��
��3�����c(di��n)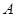 ��ƽ��
��ƽ��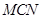 �ľ��x��
�ľ��x��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com