【答案】
分析:(1)根據f
n(x)=
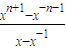
,y=x+
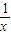
,代入yf
n(x)-f
n-1(x),化簡即可得證;
(2)先證明命題對n=1,2成立,再設n≤m(m≥2,m為正整數,命題成立,現證命題對于n=m+1成立,分類討論:①m為偶數,則m+1為奇數;②若m為奇數,則m+1為偶數,由歸納假設,即可證得結論.
解答:證明:(1)∵f
n(x)=
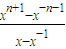
,y=x+
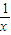
∴yf
n(x)-f
n-1(x)=(x+
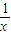
)×
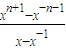
-
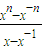
=
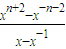
=f
n+1(x)
(2)f
1(x)=x+
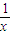
,f
2(x)=x
2+1+x
-2=y
2-1,故命題對n=1,2成立
設n=m(m≥2,m為正整數,命題成立,現證命題對于n=m+1成立
①m為偶數,則m+1為奇數,由歸納假設知,對于n=m及n=m-1,有
f
m(x)=y
m-
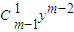
+…+…+(-1)
i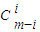
y
m-2i+…+
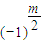
①
f
m-1(x)=y
m-1-
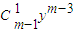
+…+(-1)
i-1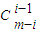
y
m+1-2i+…+
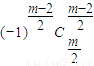
y ②
∴yf
m(x)-f
m-1(x)=y
m+1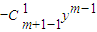
+…+(-1)
i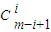
y
m+1-2i+…+
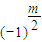
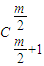
y
即命題對n=m+1成立.
②若m為奇數,則m+1為偶數,由歸納假設知,對于n=m及n=m-1,有
f
m(x)=y
m-1-
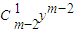
+…+…+(-1)
i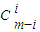
y
m-2i+…+
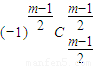
y③
f
m-1(x)=y
m-1-

+…+(-1)
i-1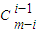
y
m+1-2i+…+
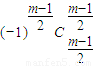
④
用y乘③減去④,同上合并,并注意最后一項常數項為-
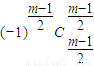
=
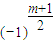
.
于是得到yf
m(x)-f
m-1(x)=y
m+1-C
m1y
m-1+…+
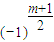
,即仍有對于n=m+1,命題成立
綜上所述,知對于一切正整數n,命題成立.
點評:本題考查數學歸納法,考查分類討論的數學思想,考查學生的計算能力,難度較大.

 (x≠0,±1),令y=x+
(x≠0,±1),令y=x+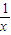 .
.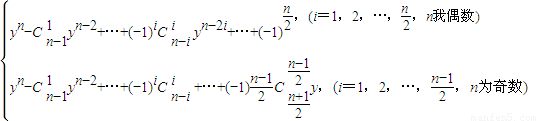 .
.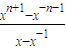 ,y=x+
,y=x+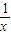 ,代入yfn(x)-fn-1(x),化簡即可得證;
,代入yfn(x)-fn-1(x),化簡即可得證;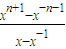 ,y=x+
,y=x+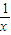
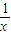 )×
)×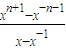 -
-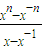 =
=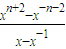 =fn+1(x)
=fn+1(x) ,f2(x)=x2+1+x-2=y2-1,故命題對n=1,2成立
,f2(x)=x2+1+x-2=y2-1,故命題對n=1,2成立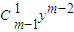 +…+…+(-1)i
+…+…+(-1)i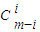 ym-2i+…+
ym-2i+…+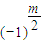 ①
①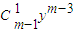 +…+(-1)i-1
+…+(-1)i-1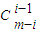 ym+1-2i+…+
ym+1-2i+…+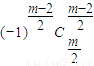 y ②
y ②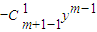 +…+(-1)i
+…+(-1)i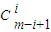 ym+1-2i+…+
ym+1-2i+…+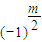
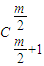 y
y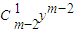 +…+…+(-1)i
+…+…+(-1)i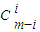 ym-2i+…+
ym-2i+…+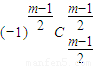 y③
y③ +…+(-1)i-1
+…+(-1)i-1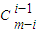 ym+1-2i+…+
ym+1-2i+…+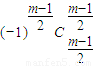 ④
④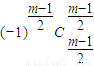 =
=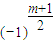 .
.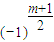 ,即仍有對于n=m+1,命題成立
,即仍有對于n=m+1,命題成立
