
寫出下列函數的單調增區間:
(1)y=3sin(2x-![]() );(2)y=2cos(2x+
);(2)y=2cos(2x+![]() );(3)y=logi[sin(2x+
);(3)y=logi[sin(2x+![]() )].
)].
|
思路分析:應用正、余弦函數的單調性.(1)設z=2x- 解:(1)設z=2x- 即2x- 由- 得- 即- 所以,函數y=3sin(2x- (2)由-π+2kπ≤2x+ 即- 所以,函數y=2cos(2x+ (3)設u=sin(2x+ 由y=sinx(y>0)的圖象,可知y=sinx(y>0)的增區間為(2kπ,2kπ+ 2kπ<2x+ 所以- 所以,函數y=log2[sin(2x+ 方法歸納:本題的關鍵在于轉化思想的應用,使用了整體換元法.函數的單調性是函數在定義域內的某個區間上的性質,因此,要求函數的單調區間,應首先求函數的定義域.此外,函數的單調區間應寫成區間的形式. |


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源:2010年江蘇省高一第一學期階段測試數學試卷 題型:填空題
下列結論中:
①定義在R上的函數f(x)在區間(-∞,0]上是增函數,在區間(0,+∞)也是增函數,則函數f(x)在R上是增函數;
②若f(2)=f(-2),則函數f(x)不是奇函數;
③函數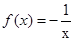 的單調增區間是(-∞,0)
的單調增區間是(-∞,0) (0,+∞)
(0,+∞)
④對應法則和值域相同的函數的定義域也相同;
⑤函數的定義域一定不是空集; 寫出上述所有正確結論的序號: ▲ .
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
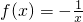 的單調增區間是(-∞,0)∪(0,+∞)
的單調增區間是(-∞,0)∪(0,+∞)查看答案和解析>>
科目:高中數學 來源:2010年江蘇省沭陽中學高一第一學期階段測試數學試卷 題型:填空題
下列結論中:
①定義在R上的函數f(x)在區間(-∞,0]上是增函數,在區間(0,+∞)也是增函數,則函數f(x)在R上是增函數;
②若f(2)=f(-2),則函數f(x)不是奇函數;
③函數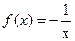 的單調增區間是(-∞,0)
的單調增區間是(-∞,0)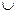 (0,+∞)
(0,+∞)
④對應法則和值域相同的函數的定義域也相同;
⑤函數的定義域一定不是空集; 寫出上述所有正確結論的序號: ▲ .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com