
已知冪函數(shù)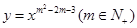 的圖象與x軸,y軸無交點且關于原點對稱,又有函數(shù)f(x)=x2-alnx+m-2在(1,2]上是增函數(shù),g(x)=x-
的圖象與x軸,y軸無交點且關于原點對稱,又有函數(shù)f(x)=x2-alnx+m-2在(1,2]上是增函數(shù),g(x)=x- 在(0,1)上為減函數(shù).
在(0,1)上為減函數(shù).
①求a的值;
②若 ,數(shù)列{an}滿足a1=1,an+1=p(an),(n∈N+),數(shù)列{bn},滿足
,數(shù)列{an}滿足a1=1,an+1=p(an),(n∈N+),數(shù)列{bn},滿足 ,
,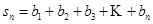 ,求數(shù)列{an}的通項公式an和sn.
,求數(shù)列{an}的通項公式an和sn.
③設 ,試比較[h(x)]n+2與h(xn)+2n的大小(n∈N+),并說明理由.
,試比較[h(x)]n+2與h(xn)+2n的大小(n∈N+),并說明理由.
①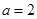 ;②
;②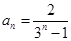 ;
;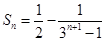 ;③見解析.
;③見解析.
【解析】
試題分析:①由冪函數(shù)的定義和性質可以知道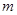 的取值集合,由圖像關于原點對稱的函數(shù)是奇函數(shù)可以確定
的取值集合,由圖像關于原點對稱的函數(shù)是奇函數(shù)可以確定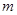 的值,將
的值,將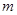 的值代入
的值代入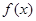 ,
,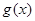 的解析式后,根據(jù)函數(shù)的單調性與導函數(shù)的關系以及不等式的恒成立問題的解法就可以知道
的解析式后,根據(jù)函數(shù)的單調性與導函數(shù)的關系以及不等式的恒成立問題的解法就可以知道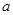 滿足的不等式,就可以解得
滿足的不等式,就可以解得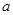 的值;②先由已知條件求出
的值;②先由已知條件求出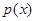 的解析式,然后得出
的解析式,然后得出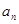 ,
,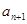 的關系,由函數(shù)構造的方法可以求得
的關系,由函數(shù)構造的方法可以求得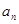 的解析式,代入
的解析式,代入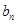 即可,再由數(shù)列求和公式求得
即可,再由數(shù)列求和公式求得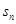 的值;③先求出
的值;③先求出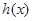 的解析式,再由相減的方法來判斷兩個式子的大小,最后減得的結果和0比較即可,注意分類討論的思想.
的解析式,再由相減的方法來判斷兩個式子的大小,最后減得的結果和0比較即可,注意分類討論的思想.
試題解析:①冪函數(shù)的圖像與 軸,
軸,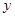 軸無交點,則有
軸無交點,則有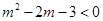 ,解得
,解得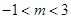
又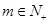 ,∴
,∴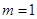 或
或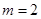 ,
,
又冪函數(shù)的圖像關于原點對稱,則有冪函數(shù)是奇函數(shù),
當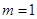 時,
時,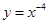 是偶函數(shù),不合題意,舍去,
是偶函數(shù),不合題意,舍去,
當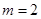 時,
時,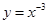 是奇函數(shù),∴
是奇函數(shù),∴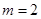 ,
,
∴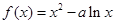 ,求導得
,求導得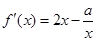 ,
,
又∵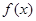 在
在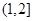 上是增函數(shù),∴
上是增函數(shù),∴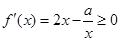 在
在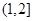 上恒成立,
上恒成立,
解得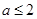 ,
,
又∵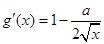 ,
,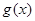 在
在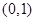 上為減函數(shù),
上為減函數(shù),
∴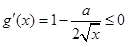 在
在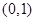 上恒成立,
上恒成立,
解得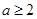 ,
,
綜上知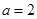 ;
..3分
;
..3分
②∵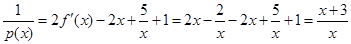 ,
,
∴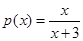 ∴
∴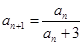 ∴
∴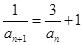 ∴
∴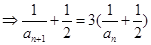 ,
,
∴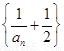 是首項為
是首項為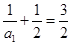 公比
公比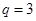 的等比數(shù)列,
的等比數(shù)列,
∴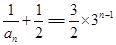 解得
解得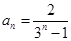 ,
,
∴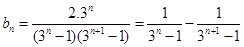 ,
,
∴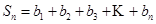 ,
,
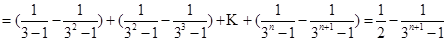 ;
.6分
;
.6分
③∵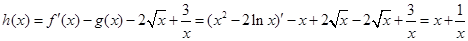 ,
,
當 時,
時,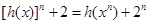 ,
,
當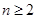 時,
時,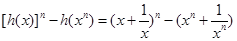
=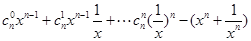
=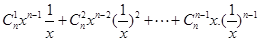
=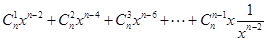
=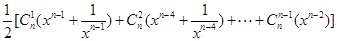
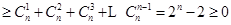 ,
,
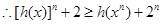 .
10分
.
10分
考點:函數(shù)的單調性與導函數(shù)的關系,奇函數(shù)圖像的性質,等比數(shù)列的構造.


科目:高中數(shù)學 來源:2011-2012學年江蘇省鎮(zhèn)江一中高一(上)期中數(shù)學試卷(解析版) 題型:填空題
 的圖象與x軸、y軸無交點且關于原點對稱,則m= .
的圖象與x軸、y軸無交點且關于原點對稱,則m= .查看答案和解析>>
科目:高中數(shù)學 來源:2010-2011學年廣東省茂名市高州市長坡中學高三(上)第二次月考數(shù)學試卷(解析版) 題型:選擇題
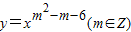 的圖象與x軸無公共點,則m的值的取值范圍是( )
的圖象與x軸無公共點,則m的值的取值范圍是( )查看答案和解析>>
科目:高中數(shù)學 來源:2011年福建省高考60天沖刺訓練數(shù)學試卷07(理科)(解析版) 題型:解答題
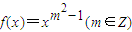 的圖象與x軸,y軸都無交點,且關于原點對稱,則函數(shù)f(x)的解析式是 .
的圖象與x軸,y軸都無交點,且關于原點對稱,則函數(shù)f(x)的解析式是 .查看答案和解析>>
科目:高中數(shù)學 來源:2011年高三數(shù)學第一輪基礎知識訓練(07)(解析版) 題型:解答題
 的圖象與x軸,y軸都無交點,且關于原點對稱,則函數(shù)f(x)的解析式是 .
的圖象與x軸,y軸都無交點,且關于原點對稱,則函數(shù)f(x)的解析式是 .查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com