
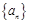 是首項為1,公差為
是首項為1,公差為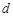 的等差數列,數列
的等差數列,數列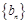 是首項為1,公比為
是首項為1,公比為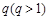 的等比
的等比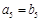 ,
,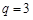 ,求數列
,求數列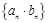 的前
的前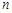 項和;
項和;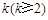 ,使得
,使得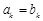 .試比較
.試比較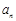 與
與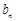 的大小,并說明理由.
的大小,并說明理由.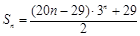 ;(2) 當
;(2) 當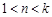 時,
時,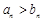 ;當
;當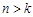 時,
時,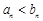 ;當
;當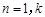 時,
時,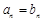 .
.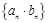 的前
的前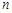 項和;(2)利用
項和;(2)利用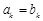 等量關系關系,減少公差d,進而將
等量關系關系,減少公差d,進而將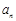 與
與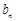 進行表示,然后才有作差比較進行分析,注意分類討論思想的應用.
進行表示,然后才有作差比較進行分析,注意分類討論思想的應用.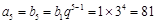 ,
, ,
,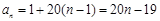 , 3分
, 3分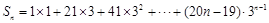 , ①
, ① , ②
, ②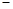 ②得,
②得,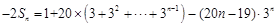 ,
,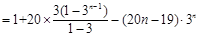
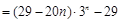 ,
,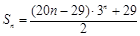 . 7分
. 7分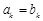 ,
,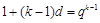 ,即
,即 ,
, ,
,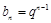 , 9分
, 9分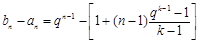
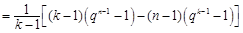
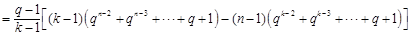
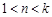 時,由
時,由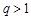 知
知
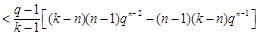
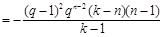
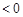 , 13分
, 13分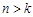 時,由
時,由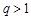 知
知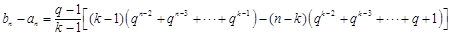
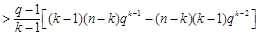
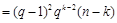
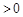 ,
,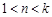 時,
時,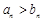 ;當
;當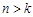 時,
時,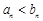 ;當
;當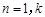 時,
時,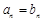 . 16分
. 16分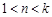 時,
時,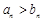 ;
;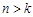 時,
時,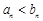 ”得2分.)
”得2分.)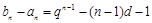 (易知
(易知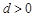 ),
),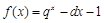 ,有
,有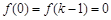 ,
,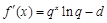 ,
,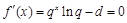 ,則
,則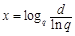 .記
.記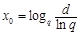 .
.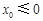 ,則在
,則在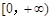 上
上 ,函數
,函數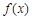 在
在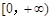 上為單調增函數,則
上為單調增函數,則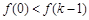 ,
,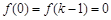 相矛盾;
相矛盾;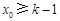 ,則在
,則在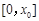 上
上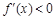 ,函數
,函數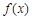 在
在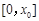 上為單調減函數,則
上為單調減函數,則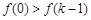 ,
,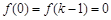 相矛盾;
相矛盾; .
.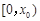 上
上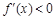 ,函數
,函數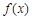 在
在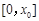 上為單調減函數,
上為單調減函數,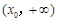 上
上 ,函數
,函數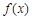 在
在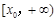 上為單調增函數.
上為單調增函數.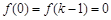 ,所以,當
,所以,當 時,
時,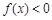 ,當
,當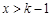 時,
時,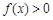 ,
,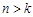 時,
時,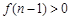 ,即
,即 ,
,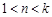 時,
時,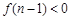 ,即
,即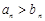 ,
,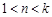 時,
時,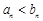 ;當
;當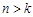 時,
時,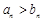 ;當
;當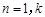 時,
時,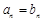 .
.

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com