
從6名短跑運動員中選出4人參加4×100 m接力賽.試求滿足下列條件的參賽方案各有多少種?
(1)甲不能跑第一棒和第四棒;
(2)甲不能跑第一棒,乙不能跑第四棒
(1)240;(2)252;
解析試題分析:(1)可優先考慮特殊元素甲,此時務必注意甲是否參賽,因此需分兩類,甲參賽和甲不參賽,利用分類加法計數原理求解
(2)顯然第一、四棒為特殊位置,與之相伴的甲、乙則為特殊元素,這時特殊元素與特殊位置的個數相等,利用特殊位置(元素)優先考慮的原則解之.
(1)優先考慮特殊元素甲,讓其選位置,此時務必注意甲是否參賽,因此需分兩類:
第1類,甲不參賽有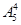 種排法;
種排法;
第2類,甲參賽,因只有兩個位置可供選擇,故有A種排法;其余5人占3個位置有A種排法,故有AA種方案.所以有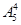 +
+
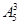 =240種參賽方案.
=240種參賽方案.
(2)優先考慮特殊位置.
第1類,乙跑第一棒有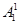
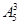 =60種排法;
=60種排法;
第2類,乙不跑第一棒有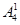
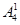
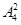 =192種排法.
=192種排法.
故共有60+192=252種參賽方案.
考點:排列組合,計數原理


科目:高中數學 來源: 題型:解答題
6個人坐在一排10個座位上,則(用數字表示).
(1)空位不相鄰的坐法有多少種?
(2)4個空位只有3個相鄰的坐法有多少種?
(3)4個空位至多有2個相鄰的坐法有多少種?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知(1+x)n=a0+a1(x-1)+a2(x-1)2+…+an(x-1)n(n∈N*).
(1)求a0及Sn=a1+a2+a3+…+an;
(2)試比較Sn與(n-2)2n+2n2的大小,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工程隊有6項工程需要先后單獨完成,其中工程乙必須在工程甲完成后才能進行,工程丙必須在工程乙完成后才能進行,又工程丁必須在工程丙完成后立即進行.求安排這6項工程的不同排法種數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com