
已知動圓 經過點
經過點 和
和
(Ⅰ)當圓 面積最小時,求圓
面積最小時,求圓 的方程;
的方程;
(Ⅱ)若圓 的圓心在直線
的圓心在直線 上,求圓
上,求圓 的方程。
的方程。
(Ⅰ) (Ⅱ)
(Ⅱ)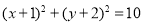
【解析】
試題分析:(Ⅰ)圓面積決定于半徑,所以當半徑最小時,圓面積最小 圓過A,B,則AB為圓中的弦,當AB為圓直徑時,圓的半徑最小 本題實質是求以AB為直徑的圓的方程,(Ⅱ)圓心不僅在直線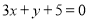 上,而且也在線段AB中垂線上,這兩條直線的交點就是圓心,有了圓心就可求半徑了 這是幾何方法,如從圓的標準方程出發則列出三個獨立的方程,解方程組的順序應為先消去半徑
上,而且也在線段AB中垂線上,這兩條直線的交點就是圓心,有了圓心就可求半徑了 這是幾何方法,如從圓的標準方程出發則列出三個獨立的方程,解方程組的順序應為先消去半徑 ,其實質就是線段AB中垂線方程
,其實質就是線段AB中垂線方程
試題解析:(Ⅰ)要使圓 的面積最小,則
的面積最小,則 為圓
為圓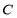 的直徑, 2分
的直徑, 2分
圓心 ,半徑
,半徑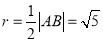 4分
4分
所以所求圓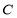 的方程為:
的方程為: 6分
6分
(Ⅱ)法一:因為 ,
, 中點為
中點為 ,
,
所以 中垂線方程為
中垂線方程為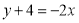 ,即
,即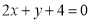 8分
8分
解方程組 得:
得: ,所以圓心
,所以圓心 為
為 10分
10分
根據兩點間的距離公式,得半徑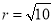 , 11分
, 11分
因此,所求的圓 的方程為
的方程為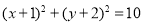 12分
12分
法二:設所求圓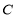 的方程為
的方程為 ,
,
根據已知條件得
 6分
6分
 11分
11分
所以所求圓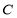 的方程為
的方程為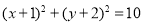 12分
12分
考點:圓的標準方程


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:高中數學 來源:2016屆山東棗莊第三中學高一第一學期期末考試數學試卷(解析版) 題型:選擇題
在下列命題中,不是公理的是( )
A.平行于同一個平面的兩個平面平行
B.過不在同一直線上的三個點,有且只有一個平面
C.如果一條直線上的兩點在同一個平面內,那么這條直線上所有點都在此平面內
D.如果兩個不重合的平面有一個公共點,那么它們有且只有一條過該點的公共直線
查看答案和解析>>
科目:高中數學 來源:2016屆安徽渦陽四中蒙城六中高一上學期期末聯考數學卷(解析版) 題型:選擇題
設m、n是兩條不同的直線, 是三個不同的平面,給出下列四個命題:
是三個不同的平面,給出下列四個命題:
①若 ,
, ,則
,則 ②若
②若 ,
, ,
, ,則
,則
③若 ,
, ,則
,則 ④若
④若 ,
, ,則
,則
其中正確命題的序號是 ( )
A.①和② B.②和③ C.③和④ D.①和④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com