
從某節能燈生產在線隨機抽取100件產品進行壽命試驗,按連續使用時間(單位:天)共分5組,得到頻率分布直方圖如圖.
(I)以分組的中點資料作為平均數據,用樣本估計該生產線所生產的節能燈的預期連續使用壽命;
(II)為了分析使用壽命差異較大的產品,從使用壽命低于200天和高于350天的產品中用分層抽樣的方法共抽取6件,求樣品A被抽到的概率。
(I)280天(II)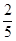
解析試題分析:(Ⅰ)樣本數據的平均數為:
175×0.05+225×0.15+275×0.55+325×0.15+375×0.1=280.
因此,該生產線所生產的節能燈的預期連續使用壽命為280天. …5分
(Ⅱ)使用壽命低于200天的一組中應抽取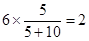 . …7分
. …7分
記使用壽命低于200天的5件產品A,B,C,D,E.
從中選出2件的不同情形為:
AB,AC,AD,AE,
BC,BD,BE,
CD,CE,
DE,
共10種可能.
其中某產品A被抽到的概率為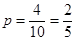 .
.
考點:頻率分布直方圖及分層抽樣古典概率
點評:頻率分布直方圖中每一個小矩形的面積等于該組的頻率,古典概型概率的求解需找到所有基本事件總數及滿足題意要求的基本事件種數,然后求其比值


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源: 題型:解答題
袋中裝有大小相同的2個白球和3個黑球.
(1)采取放回抽樣方式,從中依次摸出兩個球,求兩球顏色不同的概率;
(2)采取不放回抽樣方式,從中依次摸出兩個球,記 為摸出兩球中白球的個數,
為摸出兩球中白球的個數,
求 的期望.
的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
“H7N9禽流感”問題越來越引起社會關注,我校對高一600名學生進行了一次“H7N9禽流感”知識測試,并從中抽取了部分學生的成績(滿分100分)作為樣本,繪制了下面尚未完成的頻率分布表和頻率分布直方圖.
(1)填寫答題卡頻率分布表中的空格,補全頻率分布直方圖,并標出每個小矩形對應的縱軸數據;
(2)試估計該年段成績在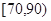 段的有多少人;
段的有多少人;
(3)請你估算該年級的平均分.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
由于某高中建設了新校區,為了交通方便要用三輛通勤車從老校區把教師接到新校區.已知從新校區到老校區有兩條公路,汽車走一號公路堵車的概率為 ,不堵車的概率為
,不堵車的概率為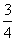 ;汽車走二號公路堵車的概率為p,不堵車的概率為1-p,若甲、乙兩輛汽車走一號公路,丙汽車由于其他原因走二號公路,且三輛車是否堵車相互之間沒有影響.
;汽車走二號公路堵車的概率為p,不堵車的概率為1-p,若甲、乙兩輛汽車走一號公路,丙汽車由于其他原因走二號公路,且三輛車是否堵車相互之間沒有影響.
(Ⅰ)若三輛汽車中恰有一輛汽車被堵的概率為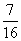 ,求走二號公路堵車的概率;
,求走二號公路堵車的概率;
(Ⅱ)在(Ⅰ)的條件下,求三輛汽車中被堵車輛的個數ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在某校組織的一次籃球定點投籃測試中,規定每人最多投 次,每次投籃的結果相互獨立.在
次,每次投籃的結果相互獨立.在 處每投進一球得
處每投進一球得 分,在
分,在 處每投進一球得
處每投進一球得 分,否則得
分,否則得 分. 將學生得分逐次累加并用
分. 將學生得分逐次累加并用 表示,如果
表示,如果 的值不低于
的值不低于 分就認為通過測試,立即停止投籃,否則繼續投籃,直到投完三次為止.投籃的方案有以下兩種:方案1:先在
分就認為通過測試,立即停止投籃,否則繼續投籃,直到投完三次為止.投籃的方案有以下兩種:方案1:先在 處投一球,以后都在
處投一球,以后都在 處投;方案2:都在
處投;方案2:都在 處投籃.甲同學在
處投籃.甲同學在 處投籃的命中率為
處投籃的命中率為 ,在
,在 處投籃的命中率為
處投籃的命中率為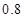 .
.
(Ⅰ)甲同學選擇方案1.
求甲同學測試結束后所得總分等于4的概率;
求甲同學測試結束后所得總分 的分布列和數學期望
的分布列和數學期望 ;
;
(Ⅱ)你認為甲同學選擇哪種方案通過測試的可能性更大?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一個袋中裝有大小相同的球10個,其中紅球8個,黑球2個,現從袋中有放回地取球,每次隨機取1個. 求:
(1)連續取兩次都是紅球的概率;
(2)如果取出黑球,則取球終止,否則繼續取球,直到取出黑球,但取球次數最多不超過4次,求取到黑球的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某廣場上有4盞裝飾燈,晚上每盞燈都隨機地閃爍紅燈或綠燈,每盞燈出現紅燈的概率都是 ,出現綠燈的概率都是
,出現綠燈的概率都是 .記這4盞燈中出現紅燈的數量為
.記這4盞燈中出現紅燈的數量為 ,當這排裝飾燈閃爍一次時:
,當這排裝飾燈閃爍一次時:
(1)求 時的概率;(2)求
時的概率;(2)求 的數學期望.
的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com