
已知 .
.
(Ⅰ)求 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(Ⅱ)若函數(shù) 在
在 上只有一個零點,求實數(shù)
上只有一個零點,求實數(shù) 的取值范圍.
的取值范圍.
(Ⅰ) 和
和 ;(Ⅱ)
;(Ⅱ) 或
或
解析試題分析:1.本題要注意函數(shù)的定義域 .2.在比較
.2.在比較 與
與 的大小時,如果直接采用作差的方式進行比較:
的大小時,如果直接采用作差的方式進行比較:
 ,則很難得出答案.實際上,因為
,則很難得出答案.實際上,因為 ,
, ,所以
,所以 .這提示我們處理問題的時候思維要相當(dāng)靈活,要眼觀六路,耳聽八方,怎么好做就怎么做.
.這提示我們處理問題的時候思維要相當(dāng)靈活,要眼觀六路,耳聽八方,怎么好做就怎么做.
3. 很多考生誤認(rèn)為 在
在 上只有一個零點
上只有一個零點 事實上漏了
事實上漏了 .
.
試題解析:(Ⅰ) 的定義域為
的定義域為 .
.
∵
∴ .
.
解 得
得 或
或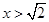 .
.
∴ 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是 和
和 .
.
(Ⅱ)由已知得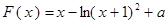 ,且
,且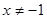 .
.
∴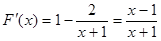 .
.
∴當(dāng) 或
或 時,
時, ;
;
當(dāng) 時,
時, .
.
∴當(dāng) 時,
時, ,此時,
,此時,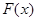 單調(diào)遞減;
單調(diào)遞減;
當(dāng)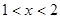 時,
時, ,此時,
,此時,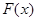 單調(diào)遞增.
單調(diào)遞增.
∵ ,
, ,
,
∴ .
.
∴ 在
在 上只有一個零點
上只有一個零點 或
或 .
.
由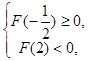 得
得 ;
;
由 ,得
,得 .
.
∴實數(shù) 的取值范圍為
的取值范圍為 或
或
考點:函數(shù)的單調(diào)性、極值、零點、比較大小.


科目:高中數(shù)學(xué) 來源: 題型:解答題
已知 ,
,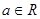
(Ⅰ)當(dāng) 時,求曲線
時,求曲線 在點
在點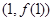 處的切線方程;
處的切線方程;
(Ⅱ)若 在
在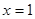 處有極值,求
處有極值,求 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(Ⅲ)是否存在實數(shù) ,使
,使 在區(qū)間
在區(qū)間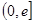 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知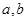 是實數(shù),函數(shù)
是實數(shù),函數(shù)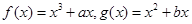 ,
,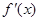 和
和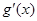 ,分別是
,分別是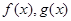 的導(dǎo)函數(shù),若
的導(dǎo)函數(shù),若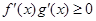 在區(qū)間
在區(qū)間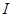 上恒成立,則稱
上恒成立,則稱 和
和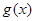 在區(qū)間
在區(qū)間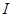 上單調(diào)性一致.
上單調(diào)性一致.
(Ⅰ)設(shè)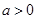 ,若函數(shù)
,若函數(shù) 和
和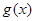 在區(qū)間
在區(qū)間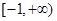 上單調(diào)性一致,求實數(shù)
上單調(diào)性一致,求實數(shù)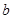 的取值范圍;
的取值范圍;
(Ⅱ)設(shè)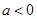 且
且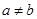 ,若函數(shù)
,若函數(shù) 和
和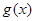 在以
在以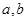 為端點的開區(qū)間上單調(diào)性一致,求
為端點的開區(qū)間上單調(diào)性一致,求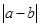 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)
(I)若函數(shù) 上是減函數(shù),求實數(shù)
上是減函數(shù),求實數(shù) 的最小值;
的最小值;
(2)若 ,使
,使 (
( )成立,求實數(shù)
)成立,求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) .
.
(Ⅰ)求函數(shù)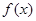 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)設(shè)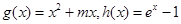 ,若在
,若在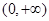 上至少存在一點
上至少存在一點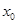 ,使得
,使得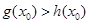 成立,求
成立,求 的范圍.
的范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) ,
, 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).
(Ⅰ)當(dāng)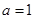 時,求
時,求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若函數(shù) 在
在 上無零點,求
上無零點,求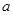 最小值;
最小值;
(Ⅲ)若對任意給定的 ,在
,在 上總存在兩個不同的
上總存在兩個不同的
 ),使
),使 成立,求
成立,求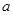 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)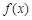 是定義在
是定義在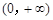 的可導(dǎo)函數(shù),且不恒為0,記
的可導(dǎo)函數(shù),且不恒為0,記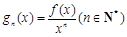 .若對定義域內(nèi)的每一個
.若對定義域內(nèi)的每一個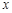 ,總有
,總有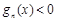 ,則稱
,則稱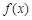 為“
為“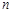 階負(fù)函數(shù)”;若對定義域內(nèi)的每一個
階負(fù)函數(shù)”;若對定義域內(nèi)的每一個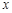 ,總有
,總有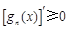 ,
,
則稱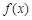 為“
為“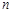 階不減函數(shù)”(
階不減函數(shù)”(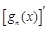 為函數(shù)
為函數(shù)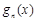 的導(dǎo)函數(shù)).
的導(dǎo)函數(shù)).
(1)若 既是“1階負(fù)函數(shù)”,又是“1階不減函數(shù)”,求實數(shù)
既是“1階負(fù)函數(shù)”,又是“1階不減函數(shù)”,求實數(shù)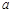 的取值范圍;
的取值范圍;
(2)對任給的“2階不減函數(shù)”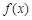 ,如果存在常數(shù)
,如果存在常數(shù)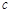 ,使得
,使得 恒成立,試判斷
恒成立,試判斷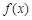 是否為“2階負(fù)函數(shù)”?并說明理由.
是否為“2階負(fù)函數(shù)”?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知 在
在 與
與 處都取得極值.
處都取得極值.
(Ⅰ) 求 ,
, 的值;
的值;
(Ⅱ)設(shè)函數(shù) ,若對任意的
,若對任意的 ,總存在
,總存在 ,使得、
,使得、 ,求實數(shù)
,求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com