如圖,

是半圓
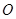
的直徑,

是半圓
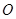
上除

、

外的一個動點,

垂直于半圓
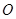
所在的平面,

∥

,

,

,

.

⑴證明:平面

平面

;
⑵當三棱錐

體積最大時,求二面角

的余弦值.
(1)要證明平面

平面

,需要通過其判定定理來得到,先證明
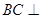
平面

,進而得到。
(2)
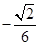
試題分析:(Ⅰ)證明:因為

是直徑,所以
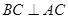
1分,
因為
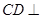
平面
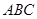
,所以
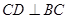
2分,
因為
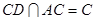
,所以
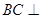
平面

3分
因為
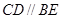
,
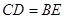
,所以
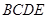
是平行四邊形,
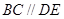
,所以
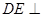
平面

4分,
因為
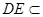
平面
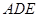
,所以平面

平面

5分
(Ⅱ)依題意,
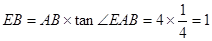
6分,
由(Ⅰ)知

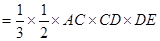
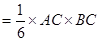
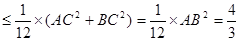
,當且僅當
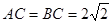
時等號成立 8分
如圖所示,建立空間直角坐標系,則
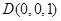
,
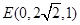
,
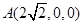

,則
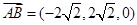
,
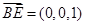
,
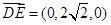
,
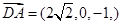
9分
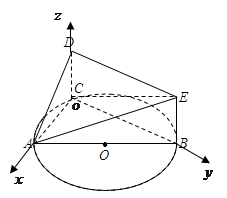
設(shè)面
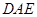
的法向量為
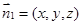
,
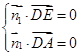
,即
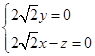
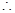
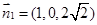
, 10分
設(shè)面
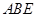
的法向量為
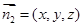
,
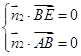
,即
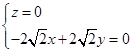
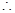
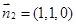
,
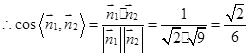
12分
可以判斷
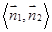
與二面角

的平面角互補
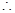
二面角

的余弦值為
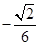
。 13分
點評:主要是考查了面面垂直和二面角的平面角的求解,屬于基礎(chǔ)題。
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,在四棱錐P-ABCD中,PA⊥平面ABCD, AB//CD,∠DAB=90°,PA=AD=DC=1,AB=2,M為PB的中點.

(I)證明:MC//平面PAD;
(II)求直線MC與平面PAC所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
與棱長為1的正方體的一條棱平行的截面中,面積最大的截面面積為 .
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
平面
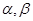
和直線
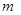
,給出條件:①
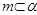
;②
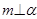
;③
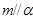
;④
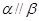
;⑤
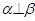
.為使
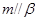
,應(yīng)選擇下面四個選項中的條件( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知在正方體
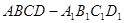
中

,

分別是

的中點,

在棱

上,且

.

(1)求證:

; (2)求二面角

的大小.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,在四棱錐
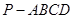
中,底面
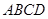
是矩形,
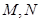
分別為
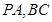
的中點,
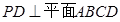
,且
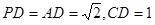
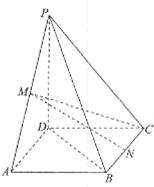
(1)證明:
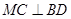
;
(2)求二面角
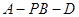
的余弦值。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
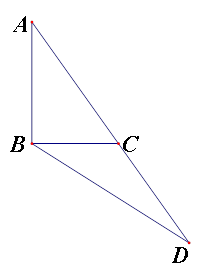
如圖,在
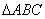
中,
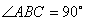
,延長
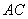
到
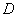
,連接
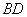
,若
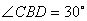
,且
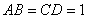
,則
________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
在棱長為2的正方體
中,設(shè)
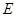
是棱
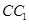
的中點.
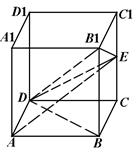
⑴ 求證:
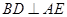
;
⑵ 求證:
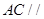
平面
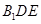
;
⑶ 求三棱錐
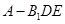
的體積.
查看答案和解析>>

 是半圓
是半圓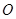 的直徑,
的直徑, 是半圓
是半圓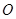 上除
上除 、
、 外的一個動點,
外的一個動點, 垂直于半圓
垂直于半圓 所在的平面,
所在的平面,  ∥
∥ ,
, ,
, ,
, .
.
 平面
平面 ;
; 體積最大時,求二面角
體積最大時,求二面角 的余弦值.
的余弦值. 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業(yè)安徽少年兒童出版社系列答案
暑假作業(yè)安徽少年兒童出版社系列答案
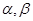 和直線
和直線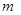 ,給出條件:①
,給出條件:①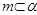 ;②
;②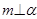 ;③
;③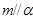 ;④
;④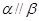 ;⑤
;⑤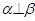 .為使
.為使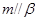 ,應(yīng)選擇下面四個選項中的條件( )
,應(yīng)選擇下面四個選項中的條件( )