
 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作業本系列答案
名校作業本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:高中數學 來源:2014年高考數學(理)二輪復習專題能力測評6練習卷(解析版) 題型:解答題
已知橢圓中心在坐標原點,焦點在x軸上,離心率為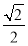 ,它的一個頂點為拋物線x2=4y的焦點.
,它的一個頂點為拋物線x2=4y的焦點.
(1)求橢圓方程;
(2)若直線y=x-1與拋物線相切于點A,求以A為圓心且與拋物線的準線相切的圓的方程;
(3)若斜率為1的直線交橢圓于M、N兩點,求△OMN面積的最大值(O為坐標原點).
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題能力測評4練習卷(解析版) 題型:填空題
對于正項數列{an},定義Hn=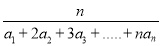 為{an}的“光陰”值,現知某數列的“光陰”值為Hn=
為{an}的“光陰”值,現知某數列的“光陰”值為Hn=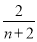 ,則數列{an}的通項公式為________.
,則數列{an}的通項公式為________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題能力測評3練習卷(解析版) 題型:填空題
在△ABC中,∠C=90°,M是BC的中點.若sin∠BAM=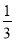 ,則sin∠BAC=________.
,則sin∠BAC=________.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題能力測評3練習卷(解析版) 題型:選擇題
將函數f(x)=sin(2x+θ)(-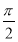 <θ<
<θ<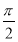 )的圖象向右平移φ(φ>0)個單位長度后得到函數g(x)的圖象,若f(x),g(x)的圖象都經過點P(0,
)的圖象向右平移φ(φ>0)個單位長度后得到函數g(x)的圖象,若f(x),g(x)的圖象都經過點P(0,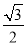 ),則φ的值可以是( ).
),則φ的值可以是( ).
A.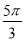 B.
B.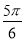 C.
C.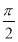 D.
D. 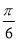
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題能力測評2練習卷(解析版) 題型:解答題
設f(x)=a(x-5)2+6ln x,其中a∈R,曲線y=f(x)在點(1,f(1))處的切線與y軸相交于點(0,6).
(1)確定a的值;
(2)求函數f(x)的單調區間與極值.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題能力測評2練習卷(解析版) 題型:選擇題
函數y=f(x)的圖象如圖所示,在區間[a,b]上可找到n(n≥2)個不同的數x1,x2,…,xn,使得 =
= =…=
=…=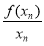 ,則n的取值范圍為( ).
,則n的取值范圍為( ).
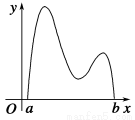
A.{3,4} B.{2,3,4} C.{3,4,5} D.{2,3}
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題能力測評1練習卷(解析版) 題型:選擇題
根據下列算法語句,當輸入x為60時,輸出y的值為( ).

A.25 B.30 C.31 D.61
查看答案和解析>>
科目:高中數學 來源:2014年高考數學(理)二輪復習專題提升訓練訓練18練習卷(解析版) 題型:解答題
經銷商經銷某種農產品,在一個銷售季度內,每售出1 t該產品獲利潤500元,未售出的產品,每1 t虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如圖所示.經銷商為下一個銷售季度購進了130 t該農產品.以X(單位:t,100≤X≤150)表示下一個銷售季度內的市場需求量,T(單位:元)表示下一個銷售季度內經銷該農產品的利潤.
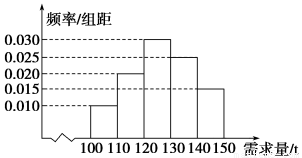
(1)將T表示為X的函數;
(2)根據直方圖估計利潤T不少于57 000元的概率;
(3)在直方圖的需求量分組中,以各組的區間中點值代表該組的各個值,并以需求量落入該區間的頻率作為需求量取該區間中點值的概率(例如:若需求量X∈[100,110),則取X=105,且X=105的概率等于需求量落入[100,110)的頻率),求T的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com