
已知橢圓C: +
+ =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ,過右焦點F的直線l與C相交于A、B兩點,當l的斜率為1時,坐標原點O到l的距離為
,過右焦點F的直線l與C相交于A、B兩點,當l的斜率為1時,坐標原點O到l的距離為 .
.
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在點P,使得當l繞F轉到某一位置時,有 =
= +
+ 成立?若存在,求出所有的P的坐標與l的方程;若不存在,說明理由.
成立?若存在,求出所有的P的坐標與l的方程;若不存在,說明理由.
(Ⅰ)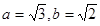 ;(Ⅱ)P(
;(Ⅱ)P(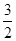 ,±
,±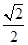 ),
),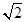 x±y-
x±y-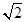 =0.
=0.
【解析】
試題分析:(Ⅰ) 先利用點到直線的距離公式求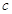 ,再利用離心率求
,再利用離心率求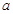 ,最后利用參數的關系求
,最后利用參數的關系求 ;(Ⅱ)設點利用方程組消元后得根與系數關系,然后代入題中條件化簡可求.
;(Ⅱ)設點利用方程組消元后得根與系數關系,然后代入題中條件化簡可求.
試題解析:(Ⅰ) 設F(c,0),當l的斜率為1時,其方程為x-y-c=0,
∴O到l的距離為 ,
,
由已知,得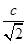 =
=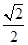 ,∴c=1.
,∴c=1.
由e=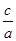 =
=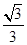 ,得a=
,得a= ,b=
,b=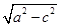 =
=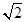 .
4分
.
4分
(Ⅱ)假設C上存在點P,使得當l繞F轉到某一位置時,有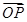 =
=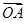 +
+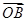 成立,
成立,
設A(x1,y1),B(x2,y2),則P(x1+x2,y1+y2).
由(Ⅰ),知C的方程為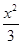 +
+ =1.
=1.
由題意知,l的斜率一定不為0,故不妨設l:x=ty+1.
由 ,消去x并化簡整理,得(2t2+3)y2+4ty-4=0.
,消去x并化簡整理,得(2t2+3)y2+4ty-4=0.
由韋達定理,得y1+y2=-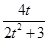 ,
,
∴x1+x2=ty1+1+ty2+1=t(y1+y2)+2=-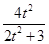 +2=
+2= ,
,
∴P( ,-
,-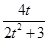 ).
).
∵點P在C上,∴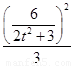 +
+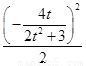 =1,
=1,
化簡整理,得4t4+4t2-3=0,即(2t2+3)(2t2-1)=0,解得t2=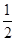 .
.
當t=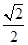 時,P(
時,P(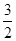 ,-
,-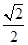 ),l的方程為
),l的方程為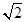 x-y-
x-y-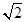 =0;
=0;
當t=-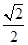 時,P(
時,P(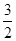 ,
,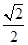 ),l的方程為
),l的方程為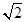 x+y-
x+y-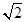 =0.
=0.
故C上存在點P(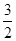 ,±
,±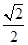 ),使
),使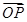 =
=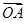 +
+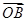 成立,此時l的方程為
成立,此時l的方程為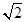 x±y-
x±y-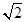 =0. 13分
=0. 13分
考點:橢圓的基本概念,點到直線的距離,根與系數關系,設而不求的思想.


 黃岡小狀元解決問題天天練系列答案
黃岡小狀元解決問題天天練系列答案 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:高中數學 來源: 題型:
(08年泉州一中適應性練習文)(12分)已知橢圓C:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,過右焦點F且斜率為1的直線交橢圓C于A,B兩點,N為弦AB的中點。
,過右焦點F且斜率為1的直線交橢圓C于A,B兩點,N為弦AB的中點。
(1)求直線ON(O為坐標原點)的斜率KON ;
(2)對于橢圓C上任意一點M ,試證:總存在角![]() (
(![]() ∈R)使等式:
∈R)使等式:![]() =cos
=cos![]()
![]() +sin
+sin![]()
![]() 成立。
成立。
查看答案和解析>>
科目:高中數學 來源: 題型:
(09年湖北重點中學4月月考理)(13分
已知橢圓C:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,過右焦點F且斜率為1的直線交橢圓C于A,B兩點,N為弦AB的
,過右焦點F且斜率為1的直線交橢圓C于A,B兩點,N為弦AB的
(1)求直線ON(O為坐標原點)的斜率KON ;
1) (2)對于橢圓C上任意一點M ,試證:總存在角![]() (
(![]() ∈R)使等式:
∈R)使等式:![]() =cos
=cos![]()
![]() +sin
+sin![]()
![]() 成立
成立
查看答案和解析>>
科目:高中數學 來源: 題型:
已知橢圓C:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,過右焦點F且斜率為1的直線交橢圓C于A,B兩點,N為弦AB的中點。
,過右焦點F且斜率為1的直線交橢圓C于A,B兩點,N為弦AB的中點。
(1)求直線ON(O為坐標原點)的斜率KON ;
(2)對于橢圓C上任意一點M ,試證:總存在角![]() (
(![]() ∈R)使等式:
∈R)使等式:![]() =cos
=cos![]()
![]() +sin
+sin![]()
![]() 成立。w.w.w.k.s.5.u.c.o.m
成立。w.w.w.k.s.5.u.c.o.m
查看答案和解析>>
科目:高中數學 來源: 題型:
已知橢圓C:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,過右焦點F且斜率為1的直線交橢圓C于A,B兩點,N為弦AB的中點。
,過右焦點F且斜率為1的直線交橢圓C于A,B兩點,N為弦AB的中點。
(1)求直線ON(O為坐標原點)的斜率KON ;
(2)對于橢圓C上任意一點M ,試證:總存在角![]() (
(![]() ∈R)使等式:
∈R)使等式:![]() =cos
=cos![]()
![]() +sin
+sin![]()
![]() 成立。
成立。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com