設(shè)
函數(shù)
滿足
.
（1）求
的單調(diào)遞減區(qū)間；
（2）設(shè)銳角
的內(nèi)角
所對的邊分別為
，且
，求
的取值范圍.
(1)
;(2)
解析試題分析：(1)由函數(shù)，運用二倍角公式的逆運算，即可將化成一個角的和差的正余弦形式.再結(jié)合基本函數(shù)的單調(diào)性，通過解不等式即可得到的單調(diào)遞減區(qū)間.
(2)因為，結(jié)合余弦定理化簡后再根據(jù)正弦定理，即可得到角B的值，又由（1）所得的函數(shù)關(guān)系，即可求出角A的范圍.
試題解析：（1）
由
得：
，∴
∴
由
得：
，
∴
的單調(diào)遞減區(qū)間為：
（2）∵
，由余弦定理得：
，
即
，由正弦定理得：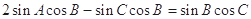
，
， 
，∴
∵△
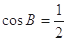銳角三角形，∴
，
∴
的取值范圍為．
考點：1.三角函數(shù)的二倍角公式.2.三角函數(shù)的化一公式.3.運用正弦定理、余弦定理解三角形.4.三角不等式的解法.
海淀黃岡名師導(dǎo)航系列答案
普通高中同步練習(xí)冊系列答案
優(yōu)翼小幫手同步口算系列答案科目：高中數(shù)學(xué) 來源： 題型：解答題
已知函數(shù)f(x)＝cos(
＋x)·cos(－x)，g(x)＝
sin2x－
．
(1)求函數(shù)f(x)的最小正周期；
(2)求函數(shù)h(x)＝f(x)－g(x)的最大值，并求使h(x)取得最大值的x的集合．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
如圖，半圓O的直徑為2，A為直徑延長線上的一點，OA＝2，B為半圓上任意一點，以AB為一邊作等邊三角形ABC.問：點B在什么位置時，四邊形OACB面積最大？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
某同學(xué)在一次研究性學(xué)習(xí)中發(fā)現(xiàn)，以下五個式子的值都等于同一個常數(shù)：
①
；
②
；
③
；
④
；
⑤
.
(1) 請根據(jù)(2)式求出這個常數(shù)；
(2)根據(jù)(1)的計算結(jié)果，將該同學(xué)的發(fā)現(xiàn)推廣為一個三角恒等式，并證明你的結(jié)論.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
已知函數(shù)
（1）求函數(shù)的最小正周期；
（2）當(dāng)
時，求函數(shù)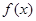
的值域；
（3）先將函數(shù)
的圖象向左平移
個單位得到函數(shù)
的圖象，再將的圖象橫坐標(biāo)擴大到原來的2倍縱坐標(biāo)不變，得到函數(shù)
的圖象，求證：直線
與的圖象相切于
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的最小正周期；
，求
的值域.
．
的值；
的值． 
，sinα＝
，tan(α－β)＝－
，求cosβ的值．
sin2
＋cos