(1)已知等差數(shù)列
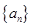
,
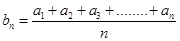
(
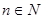
),求證:
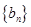
仍為等差數(shù)列;
(2)已知等比數(shù)列
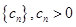
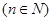
),類比上述性質(zhì),寫出一個真命題并加以證明.
(1)等差數(shù)列的定義運用,根據(jù)相鄰兩項的差為定值,來證明。
(2)若
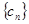
為等比數(shù)列,
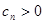
(
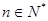
),
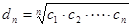
,則
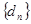
為等比數(shù)列
試題分析:證明:(1)
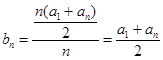
, 2分
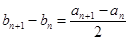
, 4分

為等差數(shù)列
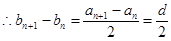
為常數(shù), 6分
所以
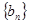
仍為等差數(shù)列; 7分
(2)類比命題:若
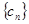
為等比數(shù)列,
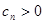
(
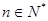
),
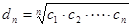
,則
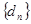
為等比數(shù)列
9分
證明:
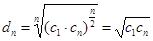
, 11分,為常數(shù), 13分
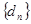
為等比數(shù)列 14分
點評:考查了類比推理的運用,以及等差數(shù)列的定義,屬于基礎題。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
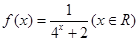
.
(1)求:
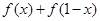
的值;
(2)類比等差數(shù)列的前
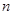
項和公式的推導方法,求:
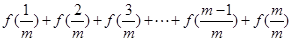
的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
等差數(shù)列

中,

;設數(shù)列

的前

項和為

,則
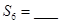
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
數(shù)列
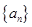
的前
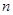
項和為
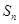
,
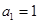
,
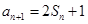
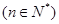
,等差數(shù)列
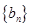
滿足
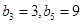
.
(1)分別求數(shù)列
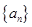
,
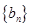
的通項公式;
(2)設
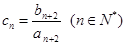
,求證
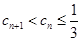
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設
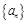
是等差數(shù)列,
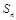
是其前
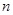
項的和,且
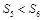
,
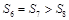
,則下列結論錯誤的是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分12分)
已知數(shù)列
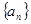
的通項公式為
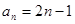
,數(shù)列
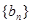
的前n項和為
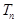
,且滿足
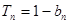
(1)求
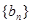
的通項公式;
(2)在
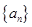
中是否存在使得
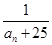
是
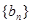
中的項,若存在,請寫出滿足題意的一項(不要求寫出所有的項);若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題共13分)
數(shù)列{
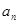
}中,
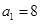
,
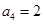
,且滿足
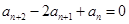
(1)求數(shù)列的通項公式;
(2)設
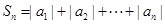
,求
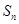
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分10分)
已知
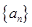
是等差數(shù)列,其中
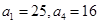
]
(1)求
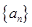
的通項;
(2)數(shù)列
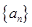
從哪一項開始小于0;
(3)求
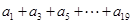
值。]
查看答案和解析>>

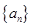 ,
,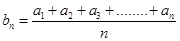 (
(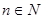 ),求證:
),求證: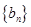 仍為等差數(shù)列;
仍為等差數(shù)列;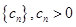
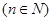 ),類比上述性質(zhì),寫出一個真命題并加以證明.
),類比上述性質(zhì),寫出一個真命題并加以證明.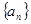 的通項公式為
的通項公式為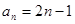 ,數(shù)列
,數(shù)列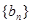 的前n項和為
的前n項和為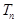 ,且滿足
,且滿足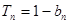
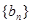 的通項公式;
的通項公式;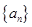 中是否存在使得
中是否存在使得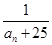 是
是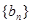 中的項,若存在,請寫出滿足題意的一項(不要求寫出所有的項);若不存在,請說明理由.
中的項,若存在,請寫出滿足題意的一項(不要求寫出所有的項);若不存在,請說明理由.