
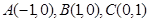 ,直線
,直線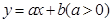 將△
將△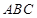 分割為面積相等的兩部分,則
分割為面積相等的兩部分,則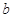 的取值范圍是( )
的取值范圍是( )A. | B. | C.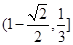 | D.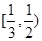 |
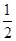 •AB•OC=1,
•AB•OC=1,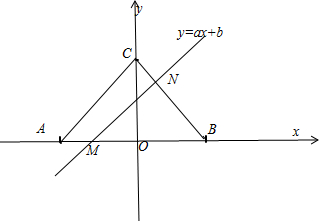
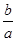 ,0),由?
,0),由?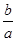 ≤0可得點M在射線OA上.
≤0可得點M在射線OA上. ,可得點N的坐標為(
,可得點N的坐標為( ),
),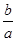 =-1,且
=-1,且 =
=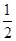 ,解得a=b=
,解得a=b= ,
,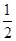 ,即
,即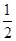 •MB•
•MB• =
=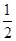 ,
,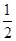 •
• =
=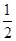 ,解得a=
,解得a=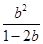 >0,故b<
>0,故b<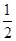 ,
,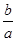 <-1,b<a,設直線y=ax+b和AC的交點為P,
<-1,b<a,設直線y=ax+b和AC的交點為P, 求得點P的坐標為(
求得點P的坐標為( ),
), ,
, ,
,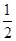 ,即
,即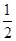 •
• •
• =
=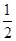 ,
, <1,則1-b<
<1,則1-b<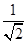 ,即b>1?
,即b>1?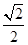 ,
, 可以,且b<
可以,且b<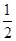 ,且b>1?
,且b>1?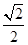 ,即b的取值范圍是(1?
,即b的取值范圍是(1?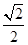 ,
,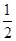 )。
)。

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com