(2014·嘉興模擬)已知a=
,b=0.3-2,c=lo
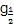2,則a,b,c的大小關系是( )
| A．a>b>c | B．a>c>b | C．c>b>a | D．b>a>c |
科目：高中數學 來源： 題型：單選題
（5分）（2011•廣東）設f（x），g（x），h（x）是R上的任意實值函數，如下定義兩個函數（f°g）（x）和（（f•g）（x）對任意x∈R，（f°g）（x）=f（g（x））；（f•g）（x）=f（x）g（x），則下列等式恒成立的是（ ）
| A．（（f°g）•h）（x）=（（f•h）°（g•h））（x） |
| B．（（f•g）°h）（x）=（（f°h）•（g°h））（x） |
| C．（（f°g）°h）（x）=（（f°h）°（g°h））（x） |
| D．（（f•g）•h）（x）=（（f•h）•（g•h））（x） |
查看答案和解析>>
科目：高中數學 來源： 題型：單選題
冪指函數y＝f(x)g(x)在求導數時，可以運用對數法：在函數解析式兩邊求對數得
，兩邊求導數得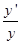
＝
，于是y′＝f(x)g(x)·．運用此法可以探求得知y＝
的一個單調遞增區間為( )．
| A．(0,2) | B．(2,3) | C．(e,4) | D．(3, 8) |
查看答案和解析>>
科目：高中數學 來源： 題型：單選題
定義：若存在常數
，使得對定義域
內的任意兩個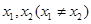
，均有
成立，則稱函數
在定義域上滿足利普希茨條件.若函數
滿足利普希茨條件，則常數的最小值為（ ）
| A．4 | B．3 | C．1 | D． |
查看答案和解析>>
科目：高中數學 來源： 題型：單選題
若直角坐標平面內的兩個不同的點
滿足條件：①都在函數
的圖象上；②關于原點對稱.則稱點對
為函數的一對“友好點對”.（注：點對與
為同一“友好點對”）.已知函數
，此函數的友好點對有（ ）
| A．0對 | B．1對 | C．2對 | D．3對 |
查看答案和解析>>
科目：高中數學 來源： 題型：單選題
已知f(x)＝ax－2，g(x)＝loga|x|(a>0，且a≠1)，且f(2 011)·g(－2 011)<0，則y＝f(x)，y＝g(x)在同一坐標系內的大致圖象是 ( )
查看答案和解析>>
科目：高中數學 來源： 題型：單選題
定義max{s1，s2，…，sn}表示實數s1，s2，…，sn中的最大者．設A＝(a1，a2，a3)，B＝
，記A?B＝max{a1b1，a2b2，a3b3}．設A＝(x－1，x＋1,1)，B＝
，若A?B＝x－1，則x的取值范圍為( )
A．[1－ ，1] |
B．[1,1＋ ] |
| C．[1－，1] |
| D．[1,1＋] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，若
，且
，則
的最小值為（ ）.
