如圖,已知

ABC中的兩條角平分線

和
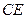
相交于

,

B=60

,

在

上,且

。
(1)證明:

四點共圓;
(2)證明:CE平分

DEF。

(Ⅰ)在△ABC中,因為∠B=60°,
所以∠BAC+∠BCA=120°.
因為AD,CE是角平分線,
所以∠HAC+∠HCA=60°,
故∠AHC=120°.
于是∠EHD=∠AHC=120°.
因為∠EBD+∠EHD=180°,
所以B,D,H,E四點共圓。
(Ⅱ)連結(jié)BH,則BH為
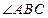
的平分線,得
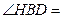
30°
由(Ⅰ)知B,D,H,E四點共圓,
所以
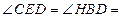
30°
又
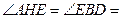
60°,由已知可得
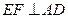
,
可得
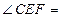
30°
所以CE平分
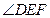
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(請考生在題22,23,24中任選一題作答,如果多做,則按所做的第一題計分。)
(本小題滿分10分)已知圓錐曲線
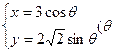
是參數(shù))和定點
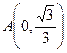
,F(xiàn)
1、F
2是圓錐曲線的左、右焦點。
(1)求經(jīng)過點F
2且垂直地于直線AF
1的直線
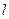
的參數(shù)方程;
(2)以坐標(biāo)原點為極點,
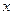
軸的正半軸為極軸建立極坐標(biāo)系,求直線AF
2的極坐標(biāo)方程。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
選答題(本小題滿分10分)(請考生在第22、23、24三道題中任選一題做答,并用2B鉛筆在答題卡上把所選題目的題號涂黑。注意所做題號必須與所涂題目的題號一致,并在答題卡指定區(qū)域答題。如果多做,則按所做的第一題計分。)
22.選修4-1:幾何證明選講
如圖,已知
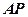
是⊙

的切線,
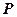
為切點,
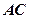
是⊙

的割線,與⊙

交于
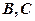
兩點,圓心

在
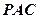
的內(nèi)部,點

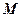
是
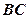
的中點。
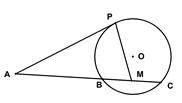
(1)證明
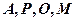
四點共圓;
(2)求
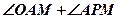
的大小。
23.選修4—4:坐標(biāo)系與參數(shù)方程
已知直線

經(jīng)過點
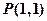
,傾斜角
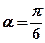
。
(1)寫出直線

的參數(shù)方程;
(2)設(shè)

與曲線
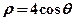
相交于兩點
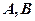
,求點
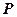
到
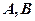
兩點的距離之積。
24.選修4—5:不等式證明選講
若不等式
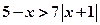
與不等式
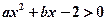
同解,而
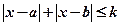
的解集為空集,求實數(shù)
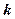
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
在極坐標(biāo)系中,已知兩點
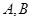
的極坐標(biāo)為
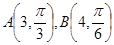
,則
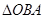
(其中
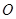
為極點)的面積為
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
點
M(3,-3,1)關(guān)于
y軸的對稱點是?( )
| A.(-3,3,-1) |
| B.(-3,-3,-1) |
| C.(3,-3,-1) |
| D.(-3,3,1) |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知直線
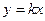
與圓
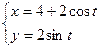
(
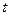
為參數(shù))相切,則直線的傾斜角為
A
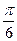
B
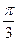

C
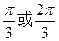
D
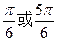
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
(幾何證明選講選做題)
如圖,已知
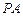
與圓
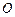
相切于
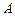
,半徑
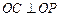
,
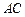
交
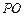
于
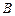
,
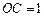
,
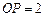
,則
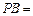 **
** .

查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
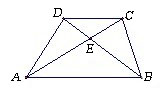
(幾何證明選講選做題) 如圖,梯形
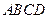
,
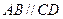
,
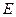
是對角線
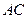
和
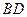
的交點,
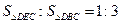
,則
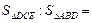
。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
直角坐標(biāo)系中,點

的極坐標(biāo)可以是
查看答案和解析>>

 ABC中的兩條角平分線
ABC中的兩條角平分線 和
和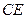 相交于
相交于 ,
, B=60
B=60 ,
, 在
在 上,且
上,且 。
。  四點共圓;
四點共圓; DEF。
DEF。
 名校課堂系列答案
名校課堂系列答案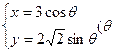 是參數(shù))和定點
是參數(shù))和定點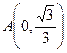 ,F(xiàn)1、F2是圓錐曲線的左、右焦點。
,F(xiàn)1、F2是圓錐曲線的左、右焦點。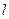 的參數(shù)方程;
的參數(shù)方程;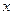 軸的正半軸為極軸建立極坐標(biāo)系,求直線AF2的極坐標(biāo)方程。
軸的正半軸為極軸建立極坐標(biāo)系,求直線AF2的極坐標(biāo)方程。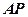 是⊙
是⊙ 的切線,
的切線,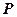 為切點,
為切點,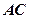 是⊙
是⊙ 的割線,與⊙
的割線,與⊙ 交于
交于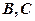 兩點,圓心
兩點,圓心 在
在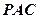 的內(nèi)部,點
的內(nèi)部,點
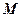 是
是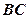 的中點。
的中點。
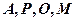 四點共圓;
四點共圓;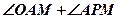 的大小。
的大小。 經(jīng)過點
經(jīng)過點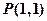 ,傾斜角
,傾斜角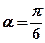 。
。 的參數(shù)方程;
的參數(shù)方程; 與曲線
與曲線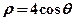 相交于兩點
相交于兩點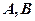 ,求點
,求點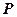 到
到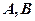 兩點的距離之積。
兩點的距離之積。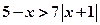 與不等式
與不等式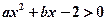 同解,而
同解,而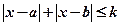 的解集為空集,求實數(shù)
的解集為空集,求實數(shù) 的取值范圍。
的取值范圍。