中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

現有下列命題：

①設a，b為正實數，若a2﹣b2=1，則a﹣b＜1；

②設，均為單位向量，若；

③數列；

④設函數，則關于x的方程f2（x）+2f（x）=0有4個解．

其中的真命題有　　．（寫出所有真命題的編號）．

【答案】①②③

【解析】①若a2﹣b2=1，則a2﹣1=b2，

即（a+1）（a﹣1）=b2，

∵a+1＞a﹣1，

∴a﹣1＜b，即a﹣b＜1，①正確；

②若，則，

即2+2cosθ＞1，cosθ＞﹣，

又∵θ∈[0，π]，

∴θ∈[0，），②正確；

③由an=n（n+4）（）n，

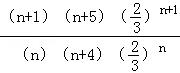令==≥1，

則2（n+1）（n+5）≥3n（n+4），

即n2≤10，所以n＜4，

即n＜4時，an+1＞an，

當n≥4時，an+1＜an，

所以a4最大，故③正確；

令f2（x）+2f（x）=0，

則f（x）=0，或f（x）=﹣2，

∵，

∴當f（x）=0時，

x=1，或x=0，或x=2，

當f（x）=﹣2時，x=10.1或x=0.99，

故方程有5個解，故④錯誤

故答案為：①②③

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

設V是已知平面M上所有向量的集合，對于映射f：V→V，a∈V，記a的象為f（a）．若映射f：V→V滿足：對所有a、b∈V及任意實數λ，μ都有f（λa+μb）=λf（a）+μf（b），則f稱為平面M上的線性變換．現有下列命題：
①設f是平面M上的線性變換，a、b∈V，則f（a+b）=f（a）+f（b）；
②若e是平面M上的單位向量，對a∈V，設f（a）=a+e，則f是平面M上的線性變換；
③對a∈V，設f（a）=-a，則f是平面M上的線性變換；
④設f是平面M上的線性變換，a∈V，則對任意實數k均有f（ka）=kf（a）．
其中的真命題是
 
（寫出所有真命題的編號）

查看答案和解析>>

科目：高中數學 來源： 題型：

設V是已知平面M上所有向量的集合，對于映射f：V→V，
a
∈V，記
a
的象為f(
a
)．若映射f：V→V滿足：對所有
a
，
b
∈V及任意實數λ，μ都有f(λ
a
+μ
b
)=λf(
a
)+μf(
b
)，則f稱為平面M上的線性變換．現有下列命題：
①設f是平面M上的線性變換，則f(
0
)=
0

②對
a
∈V設f(
a
)=2
a
，則f是平面M上的線性變換；
③若
e
是平面M上的單位向量，對
a
∈V設f(
a
)=
a
-
e
，則f是平面M上的線性變換；
④設f是平面M上的線性變換，
a
，
b
∈V，若
a
，
b
共線，則f(
a
)，f(
b
)也共線．
其中真命題是
 
（寫出所有真命題的序號）

查看答案和解析>>

科目：高中數學 來源： 題型：

現有下列命題：
①設a，b為正實數，若a2-b2=1，則a-b＜1；
②已知a＞2b＞0，則a2+
8
b(a-2b)
的最小值為16；
③數列{n(n+4)(
2
3
)n}中的最大項是第4項；
④設函數f(x)=
lg|x-1|，x≠1
0，x=1
，則關于x的方程f2（x）+2f（x）=0有4個解．
⑤若sinx+siny=
1
3
，則siny-cos2x的最大值是
4
3
．
其中的真命題有
①②③
①②③
．（寫出所有真命題的編號）

查看答案和解析>>

科目：高中數學 來源： 題型：

現有下列命題：
①設a，b為正實數，若a2-b2=1，則a-b＜1；
②設
a
，
b
均為單位向量，若|
a
+
b
|＞1則θ∈[0，
2π
3
)；
③數列{n(n+4)(
2
3
)n}中的最大項是第4項；
④設函數f(x)=
lg|x-1|，x≠1
0，x=1
，則關于x的方程f2（x）+2f（x）=0有4個解．
其中的真命題有
①②③
①②③
．（寫出所有真命題的編號）．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2012•四川）記[x]為不超過實數x的最大整數，例如，[2]=2，[1.5]=1，[-0.3]=-1．設a為正整數，數列{xn}滿足x1=a，xn+1=[
xn+[
a
xn
]
2
](n∈N*)，現有下列命題：
①當a=5時，數列{xn}的前3項依次為5，3，2；
②對數列{xn}都存在正整數k，當n≥k時總有xn=xk；
③當n≥1時，xn＞
a
-1；
④對某個正整數k，若xk+1≥xk，則xk=[
a
]．
其中的真命題有
①③④
①③④
．（寫出所有真命題的編號）

查看答案和解析>>

同步練習冊答案