
思路解析:an是關于n的函數,而由已知條件無法確定{an}是什么樣的數列,也就無法確定an的結構形式,因此不能用待定系數法來求an,解題的突破口應選定在對數列{bn}和{cn}的分析上.由條件可列出關于an+1與an的兩個等式,把它們看作關于an、an+1的方程組,即可求得an.
解:∵a1=![]() ,a2=
,a2=![]() ,
,
∴b1=log2(a2-![]() )=log2(
)=log2(![]() )=-2.
)=-2.
c1=a2-![]()
∵{bn}是公差為-1的等差數列,{cn}是公比為![]() 的等比數列,
的等比數列,
∴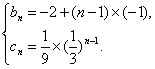
即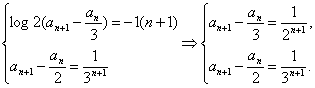
消去an+1,得an=![]() ,這就是{an}的通項公式,
,這就是{an}的通項公式,
且Sn=a1+a2+…+an=3×(![]() +
+![]() +…+
+…+![]() )+2×(
)+2×(![]() +
+![]() +…+
+…+![]() )=3×
)=3×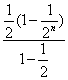 +2×
+2×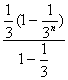 =3-
=3-![]() =2-
=2-![]() .
.
深化升華
本題主要考查了兩方面問題.一方面用函數觀點來理解數列:求通項an就是求函數解析式;另一方面是如何求這個關于n的未知函數.
在事先無法確定此函數的結構形式時,我們只能列出關于這個未知函數的方程式或方程組求解.


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:高中數學 來源: 題型:
A.a1 ,a50 B.a1,a8 C.a8,a9 D.a9,a50
查看答案和解析>>
科目:高中數學 來源: 題型:
已知數列{an}中,![]() ,
, ![]()
![]() ,
,
(1)設計一個包含循環結構的框圖,表示求![]() 算法,并寫出相應的算法語句.
算法,并寫出相應的算法語句.
(2)設計框圖,表示求數列{an}的前100項和S100的算法.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com