
已知函數(shù)f(x)=()x,
函數(shù)y=f-1(x)是函數(shù)y=f(x)的反函數(shù).
(1)若函數(shù)y=f-1(mx2+mx+1)的定義域?yàn)镽,求實(shí)數(shù)m的取值范圍;
(2)當(dāng)x∈[-1,1]時,求函數(shù)y=[f(x)]2-2af(x)+3的最小值g(a);
(3)是否存在實(shí)數(shù)m>n>3,使得g(x)的定義域?yàn)閇n,m],值域?yàn)閇n2,m2]?若存在,求出m、n的值;若不存在,請說明理由
(1)∵f-1(x)
=logx(x>0),
∴f-1(mx2+mx+1)
=log(mx2+mx+1),由題知,mx2+mx+1>0恒成立,
∴①當(dāng)m=0時,1>0滿足題意;
②當(dāng)m≠0時,
應(yīng)有
⇒0<m<4,
∴實(shí)數(shù)m的取值范圍為
0≤m<4.
(2)∵x∈[-1,1],
∴()x∈[,3],
y=[f(x)]2-2af(x)+3
=[()x]2-2a()x+3
=[()x-a]2+3-a2,
當(dāng)a<時,
ymin=g(a)=-;
當(dāng)≤a≤3時,
ymin=g(a)=3-a2;
當(dāng)a>3時,ymin=g(a)
=12-6a.
∴g(a)
=
(3)∵m>n>3,且g(x)=12-6x在(3,+∞)上是減函數(shù).
又g(x)的定義域?yàn)閇n,m],值域?yàn)閇n2,m2].
∴
②-①得:6(m-n)=(m+n)(m-n)
∵m>n>3,∴m+n=6.但這與“m>n>3”矛盾.
∴滿足題意的m、n不存在.
解析



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
有時可用函數(shù)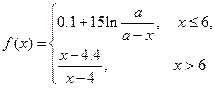
述學(xué)習(xí)某學(xué)科知識的掌握程度.其中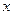 表示某學(xué)科知識的學(xué)習(xí)次數(shù)(
表示某學(xué)科知識的學(xué)習(xí)次數(shù)(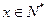 ),
),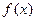 表示對該學(xué)科知識的掌握程度,正實(shí)數(shù)a與學(xué)科知識有關(guān)
表示對該學(xué)科知識的掌握程度,正實(shí)數(shù)a與學(xué)科知識有關(guān)
(1)證明:當(dāng)x 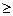 7時,掌握程度的增長量f(x+1)- f(x)總是下降;
7時,掌握程度的增長量f(x+1)- f(x)總是下降;
(2)根據(jù)經(jīng)驗(yàn),學(xué)科甲、乙、丙對應(yīng)的a的取值區(qū)間分別為(115,121],(12 1,127]
1,127]
(127,133].當(dāng)學(xué)習(xí)某學(xué)科知識6次時,掌握程度是 85%,請
85%,請 確定相應(yīng)的學(xué)科.
確定相應(yīng)的學(xué)科.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
f (x)是偶函數(shù),且在(0,+∞)上是增函數(shù),若x∈[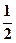 ,1]時,不等式f (ax+1)≤f (x-2)恒成立,則求實(shí)數(shù)a的取值范圍?
,1]時,不等式f (ax+1)≤f (x-2)恒成立,則求實(shí)數(shù)a的取值范圍?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知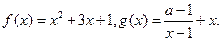
(I)a=2時,求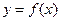 和
和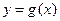 的公共點(diǎn)個數(shù);
的公共點(diǎn)個數(shù);
(II)a為何值時,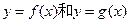 的公共點(diǎn)個數(shù)恰為兩個。
的公共點(diǎn)個數(shù)恰為兩個。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
已知f(x)、g(x)分別為奇函數(shù)、偶函數(shù),且f(x)+g(x)=2x+2x,求f(x)、g(x)的解析式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
隨著機(jī)構(gòu)改革工作的深入進(jìn)行,各單位要減員增效,有一家公司現(xiàn)有職員2a人(140<2a<420,且a為偶數(shù) ,每人每年可創(chuàng)利10萬元.據(jù)評估,在經(jīng)營條件不變的前提下,若裁員x人,則留崗職員每人每年多創(chuàng)利0.1x萬元,但公司需付下崗職員每人每年4萬元的生活費(fèi),并且該公司正常運(yùn)轉(zhuǎn)情況下,所裁人數(shù)不超過50人,為獲得最大的經(jīng)濟(jì)效益,該公司應(yīng)裁員多少人?
,每人每年可創(chuàng)利10萬元.據(jù)評估,在經(jīng)營條件不變的前提下,若裁員x人,則留崗職員每人每年多創(chuàng)利0.1x萬元,但公司需付下崗職員每人每年4萬元的生活費(fèi),并且該公司正常運(yùn)轉(zhuǎn)情況下,所裁人數(shù)不超過50人,為獲得最大的經(jīng)濟(jì)效益,該公司應(yīng)裁員多少人?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com