中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

已知圓M：及定點，點P是圓M上的動點，點Q在NP上，點G在MP上，且滿足

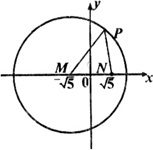
(1)求點G的軌跡C的方程；

(2)過點K(2，0)作直線l，與曲線C交于A、B兩點，O是坐標原點，設是否存在這樣的直線l，使四邊形OASB的對角線相等？若存在，求出直線l，的方程；若不存在，說明理由．

答案：
解析：

　　(1)由為PN的中點，且是PN的中垂線，

　　，

　　∴＞＞　　(4分)

　　∴點G的軌跡是以M、N為焦點的橢圓，又

　　∴　　(6分)

　　(2)∵．四邊形OASB為平行四邊行，假設存在直線1，使

　　四邊形OASB為矩形若1的斜率不存在，則1的方程為

　　由＞0．這與相矛盾，

∴1的斜率存在　　(8分)

　　設直線1的方程

　　

　　∴　　(10分)

　　∴

　　由∴　　(13分)

　　∴存在直線1：或滿足條件　　(14分)


練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

已知圓M：（x-m）2+（y-n）2=γ2及定點N（1，0），點P是圓M上的動點，點Q在NP上，點G在MP上，且滿足
NP
=2
NQ
，
GQ
•
NP
=0．
（Ⅰ）若m=-1，n=0，r=4，求點G的軌跡C的方程；
（Ⅱ）若動圓M和（Ⅰ）中所求軌跡C相交于不同兩點A、B，是否存在一組正實數m，n，r使得直線MN垂直平分線段AB，若存在，求出這組正實數；若不存在，說明理由．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知圓M的方程為：（x+3）2+y2=100及定點N（3，0），動點P在圓M上運動，線段PN的垂直平分線交圓M的半徑MP于Q點，設點Q的軌跡為曲線C，則曲線C的方程是
x2
25
+
y2
16
=1
x2
25
+
y2
16
=1
．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知圓M：（x+1）2+y2=16及定點N（1，0），點P是圓M上的動點，線段PN的中垂線與線段PM相交于點G，則點G的軌跡C的方程為
x2
4
+
y2
3
=1
x2
4
+
y2
3
=1
．

查看答案和解析>>

科目：高中數學 來源：2011-2012學年山東省煙臺市高三年級期末考試文科數學 題型：解答題

.（本小題滿分14分）

已知圓M：及定點，點P是圓M上的動點，點Q在NP上，點G在MP上，且滿足

（1）求點G的軌跡C的方程；

（2）過點K（2，0）作直線與曲線C交于A、B兩點，O是坐標原點，設是否存在這樣的直線使四邊形OASB的對角線相等？若存在，求出直線的方程；若不存在，說明理由.

 

 

 

查看答案和解析>>

同步練習冊答案