
某企業在第1年初購買一臺價值為120萬元的設備M,M的價值在使用過程中逐年減少.從第2年到第6年,每年初M的價值比上年初減少10萬元;從第7年開始,每年初M的價值為上年初的75%.
(1)求第n年初M的價值an的表達式;
(2)求數列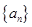 的前n項和
的前n項和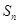
(1)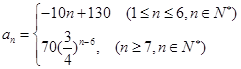 (2)
(2)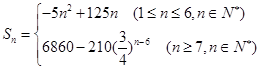
解析試題分析:(I)通過對n的分段討論,得到一個等差數列和一個等比數列,利用等差數列的通項公式及等比數列的通項公式求出第n年初M的價值an的表達式;解:(I)當n<6時,數列{an}是首項為120,公差為-10的等差數列
an=120-10(n-1)=130-10n,當n≥6時,數列{an}是以a6為首項,公比為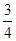 的等比數列,又a6=70,所以an=
的等比數列,又a6=70,所以an=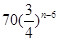 因此,第n年初,M的價值an的表達式為
因此,第n年初,M的價值an的表達式為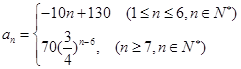
(2)然后利用分類討論的思想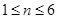 ,和
,和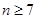 來分別求解,結合等差數列和等比數列的求和公式來的餓到,當
來分別求解,結合等差數列和等比數列的求和公式來的餓到,當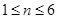 ,
,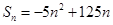 ,
,
當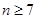 ,
,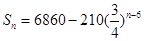 ,
,
故可知
考點:等差數列、等比數列
點評:本題考查等差數列的通項公式,前n項和公式、考查等比數列的通項公式及前n項和公式、考查分段函數的問題要分到研究


 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:高中數學 來源: 題型:解答題
已知函數 .
.
(1)若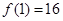 ,函數
,函數 是R上的奇函數,當
是R上的奇函數,當 時
時 ,
,
(i)求實數 與
與 的值;
的值;
(ii)當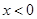 時,求
時,求 的解析式;
的解析式;
(2)若方程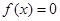 的兩根中,一根屬于區間
的兩根中,一根屬于區間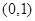 ,另一根屬于區間
,另一根屬于區間 ,求實數
,求實數 的
的
取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
統計表明,某種型號的汽車在勻速行駛中每小時的耗油量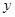 (升)關于行駛速度
(升)關于行駛速度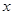 (千米/小時)的函數解析式可以表示為:
(千米/小時)的函數解析式可以表示為: 已知甲、乙兩地相距100千米.
已知甲、乙兩地相距100千米.
(1)當汽車以40千米/小時的速度勻速行駛時,從甲地到乙地要耗油多少升?
(2)當汽車以多大的速度勻速行駛時,從甲地到乙地耗油最少?最少為多少升?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
二次函數 的圖像頂點為
的圖像頂點為 ,且圖像在x軸上截得線段長為8
,且圖像在x軸上截得線段長為8
(1)求函數 的解析式;
的解析式;
(2)令
①若函數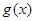 在
在 上是單調增函數,求實數
上是單調增函數,求實數 的取值范圍;
的取值范圍;
②求函數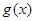 在
在 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了在夏季降溫和冬季供暖時減少能源損耗,房屋的屋頂和外墻需要建造隔熱層。某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元。該建筑物每年的能源消耗費用C(單位:萬元)與隔熱層厚度x(單位:cm)滿足關系:C(x)= 若不建隔熱層(即x=0時),每年能源消耗費用為8萬元.設f(x)為隔熱層建造費用與20年的能源消耗費用之和.
若不建隔熱層(即x=0時),每年能源消耗費用為8萬元.設f(x)為隔熱層建造費用與20年的能源消耗費用之和.
(1)求k的值;
(2)求f(x)的表達式;
(3)利用“函數 (其中
(其中 為大于0的常數),在
為大于0的常數),在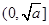 上是減函數,在
上是減函數,在 上是增函數”這一性質,求隔熱層修建多厚時,總費用f(x)達到最小,并求出這個最小值.
上是增函數”這一性質,求隔熱層修建多厚時,總費用f(x)達到最小,并求出這個最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com