
��֪����(sh��) ��
��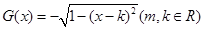
��1���� �dz���(sh��)����(w��n)��(d��ng)
�dz���(sh��)����(w��n)��(d��ng) �M��ʲô�l���r(sh��)������(sh��)
�M��ʲô�l���r(sh��)������(sh��) �����ֵ�������
�����ֵ������� ȡ���ֵ�r(sh��)
ȡ���ֵ�r(sh��) ��ֵ��
��ֵ��
��2���Ƿ���ڌ�(sh��)��(sh��)��(du��) ͬ�r(sh��)�M��l�������ף�
ͬ�r(sh��)�M��l�������ף� ȡ���ֵ�r(sh��)
ȡ���ֵ�r(sh��) ��ֵ�c
��ֵ�c ȡ��Сֵ��
ȡ��Сֵ�� ֵ��ͬ�����ң�
ֵ��ͬ�����ң� ��
��
��3���ѝM��l�����ף��Č�(sh��)��(sh��)��(du��) �ļ���ӛ��A���O(sh��)
�ļ���ӛ��A���O(sh��) ����ʹ
����ʹ ��
�� ��ȡֵ����.
��ȡֵ����.
��1�� ��ֵ��?y��n)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014030304182193759472/SYS201403030419103125339462_DA.files/image002.png">����2���C��Ҋ(ji��n)��������3�����ڣ���
��ֵ��?y��n)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014030304182193759472/SYS201403030419103125339462_DA.files/image002.png">����2���C��Ҋ(ji��n)��������3�����ڣ���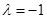 ��
��
��������
ԇ�}��������1���@��һ��(g��)����ʽ�������(w��n)�}���Ѳ���ʽ�D(zhu��n)���� ���������ô�@һ���Ƕ��β���ʽ��������ėl����
���������ô�@һ���Ƕ��β���ʽ��������ėl����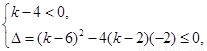 �ɽ��
�ɽ��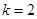 ���Ķ��õ�
���Ķ��õ�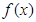 �Ľ���ʽ����ֵ��Ҳ����ã���2��Ҫ�C����(sh��)��
�Ľ���ʽ����ֵ��Ҳ����ã���2��Ҫ�C����(sh��)��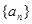 ��ԓ�^(q��)�g�����f����(sh��)�У����C
��ԓ�^(q��)�g�����f����(sh��)�У����C ��Ҳ��
��Ҳ��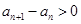 ������(j��)
������(j��)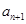 �Ķ��x���ɰ�
�Ķ��x���ɰ� �����P(gu��n)��
�����P(gu��n)��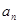 �Ķ��κ���(sh��)��������
�Ķ��κ���(sh��)��������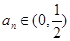 ���ɵýY(ji��)Փ
���ɵýY(ji��)Փ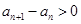 ����3���@��һ�������Ԇ�(w��n)�}����Q��(w��n)�}�ķ���һ���Ǽ��O(sh��)���ڷ����}��ĽY(ji��)Փ�����}�м��O(sh��)
����3���@��һ�������Ԇ�(w��n)�}����Q��(w��n)�}�ķ���һ���Ǽ��O(sh��)���ڷ����}��ĽY(ji��)Փ�����}�м��O(sh��)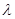 ���ڣ�ʹ����ʽ�������������
���ڣ�ʹ����ʽ�������������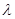 ��һ��Ҫ�Ѳ���ʽ��߅�ĺ������(l��i)���@��Ҫ���҂�Ҫ�о������һ�(xi��ng)��ʲô���@��(g��)����ʲô��(sh��)�еĺͣ���
��һ��Ҫ�Ѳ���ʽ��߅�ĺ������(l��i)���@��Ҫ���҂�Ҫ�о������һ�(xi��ng)��ʲô���@��(g��)����ʲô��(sh��)�еĺͣ���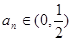 ���Ķ�
���Ķ�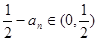 ��
��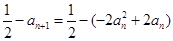
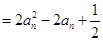
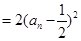 �������O(sh��)
�������O(sh��)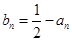 ���t
���t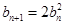 ��
��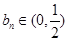 ������(du��)�@��(g��)�f�ƹ�ʽ�҂����ԃ�߅ȡ��(du��)��(sh��)�ц�(w��n)�}�D(zhu��n)����
������(du��)�@��(g��)�f�ƹ�ʽ�҂����ԃ�߅ȡ��(du��)��(sh��)�ц�(w��n)�}�D(zhu��n)����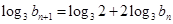 ���@�ǔ�(sh��)��
���@�ǔ�(sh��)�� ���f�ƹ�ʽ������׃?y��u)�һ��(g��)�ȱȔ�(sh��)�У���������ʽ��׃?y��u)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014030304182193759472/SYS201403030419103125339462_DA.files/image026.png">������(sh��)��
���f�ƹ�ʽ������׃?y��u)�һ��(g��)�ȱȔ�(sh��)�У���������ʽ��׃?y��u)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014030304182193759472/SYS201403030419103125339462_DA.files/image026.png">������(sh��)�� �ǹ��Ȟ�2�ĵȱȔ�(sh��)�У���ͨ�(xi��ng)��ʽ�����^(gu��)��(l��i)�������
�ǹ��Ȟ�2�ĵȱȔ�(sh��)�У���ͨ�(xi��ng)��ʽ�����^(gu��)��(l��i)�������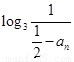 ���Ķ��������ʽ��߅�ĺͣ�����(ji��n)����ʽ��
���Ķ��������ʽ��߅�ĺͣ�����(ji��n)����ʽ��
ԇ�}��������1����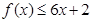 ������ȃr(ji��)��
������ȃr(ji��)�� �������
�������
�Ķ��ã�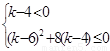 ������(ji��n)��
������(ji��n)��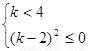 ���Ķ���
���Ķ��� ������
������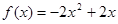 ��
��
3��
��ֵ��?y��n)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014030304182193759472/SYS201403030419103125339462_DA.files/image034.png">. 4��
��2���⣺

6��
 ��
8��
��
8��
�Ķ���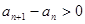 ����
����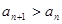 �����Ԕ�(sh��)��
�����Ԕ�(sh��)�� �څ^(q��)�g
�څ^(q��)�g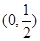 �����f����(sh��)��.
�����f����(sh��)��.
10��
��3���ɣ�2��֪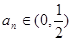 ���Ķ�
���Ķ�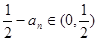 ��
��
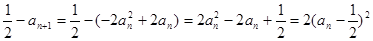 ����
����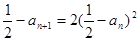 ��
��
12��
��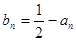 ���t��
���t��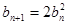 ��
��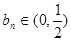 ��
��
�Ķ��� ���ɵ�
���ɵ�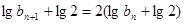 �����Ԕ�(sh��)��
�����Ԕ�(sh��)��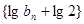 ��
�� �����(xi��ng)�����Ȟ�
�����(xi��ng)�����Ȟ� �ĵȱȔ�(sh��)�У�
�ĵȱȔ�(sh��)�У�
�Ķ���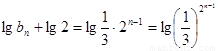 ����
����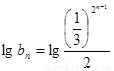 ��
��
���� 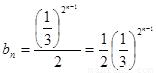 ��
��
����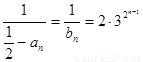 ������
������ ��
��
���ԣ�
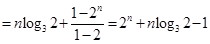 .
.
��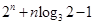
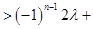
 �����ԣ�
�����ԣ�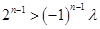 �����.
�����.
15��
��(d��ng)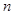 ���攵(sh��)�r(sh��)����
���攵(sh��)�r(sh��)����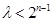 ���������(d��ng)�҃H��(d��ng)
���������(d��ng)�҃H��(d��ng) �r(sh��)��
�r(sh��)��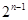 ����Сֵ
����Сֵ ��.
��.
16��
��(d��ng)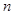 ��ż��(sh��)�r(sh��)����
��ż��(sh��)�r(sh��)����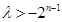 ���������(d��ng)�҃H��(d��ng)
���������(d��ng)�҃H��(d��ng)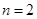 �r(sh��)�������ֵ
�r(sh��)�������ֵ ��.
��.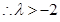
17��
���ԣ���(du��)����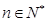 ����
����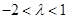 .��
.��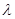 ��������(sh��)��
��������(sh��)��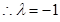
18��
���c(di��n)����1�����β���ʽ�������(w��n)�}�c����(sh��)��ֵ��2���f����(sh��)�У���3���f�ƹ�ʽ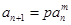 ��
��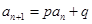 �Ĕ�(sh��)��ͨ�(xi��ng)��ʽ���ȱȔ�(sh��)�е�ǰ
�Ĕ�(sh��)��ͨ�(xi��ng)��ʽ���ȱȔ�(sh��)�е�ǰ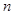 �(xi��ng)�ͣ�
�(xi��ng)�ͣ�


 ��(l��)�ŕ�(sh��)�I(y��)���㕽ӌ���������ϵ�д�
��(l��)�ŕ�(sh��)�I(y��)���㕽ӌ���������ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
����С�}�M��12�֣���֪����(sh��)![]() ��
��
��1����![]() ��ԇ�_������(sh��)
��ԇ�_������(sh��)![]() �Ć��{(di��o)�^(q��)�g����2����
�Ć��{(di��o)�^(q��)�g����2����![]() ���Ҍ�(du��)������
���Ҍ�(du��)������![]() ��
��![]() �������ԇ�_����(sh��)��(sh��)
�������ԇ�_����(sh��)��(sh��)![]() ��ȡֵ��������3���O(sh��)����(sh��)
��ȡֵ��������3���O(sh��)����(sh��)![]() �����C��
�����C��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2014�Ì��ĸ߶��όW(xu��)����ĩ��ԇ�ĿƔ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ�����}
�����}�M��12�֣���֪����(sh��) ��
��
��1���� ����
���� ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2����(d��ng) �r(sh��)�����C��
�r(sh��)�����C�� ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2012-2013�W(xu��)�����ʡ���(y��ng)�и�����һ���|(zh��)���z�y(c��)���Ɣ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ�����}
����С�}�M��13�֣���֪����(sh��)
 ��
��
��1���� ��
��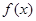 �ĘOֵ�c(di��n)����(sh��)��(sh��)
�ĘOֵ�c(di��n)����(sh��)��(sh��) ��ֵ��
��ֵ��
��2���� ��
�� �Ϟ�������(sh��)����(sh��)��(sh��)
�Ϟ�������(sh��)����(sh��)��(sh��) ��ȡֵ������
��ȡֵ������
��3����(d��ng) �r(sh��)������
�r(sh��)������ �Ќ�(sh��)������(sh��)��(sh��)
�Ќ�(sh��)������(sh��)��(sh��) �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ��2011-2012�W(xu��)�����ʡ�A�Ў���һ���и����όW(xu��)�����Йz�y(c��)�ĿƔ�(sh��)�W(xu��)ԇ���������棩 �}�ͣ�����}
��֪����(sh��) ��
��
��1���� ����(sh��)
����(sh��) ��ֵ��
��ֵ��
��2����(sh��) ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ������ʡ10-11�W(xu��)��߶��W(xu��)����ĩ��ԇ��(sh��)�W(xu��)������ �}�ͣ�����}
��֪����(sh��) ��
��
��1����ļ��� ����ȡһ��(g��)Ԫ��
����ȡһ��(g��)Ԫ�� ���ļ���
���ļ��� ����ȡһ��(g��)Ԫ��
����ȡһ��(g��)Ԫ��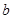 ����
���� �Ѓɂ�(g��)����Ȍ�(sh��)���ĸ��ʣ�
�Ѓɂ�(g��)����Ȍ�(sh��)���ĸ��ʣ�
��2���� �Ǐą^(q��)�g
�Ǐą^(q��)�g ����ȡ��һ��(g��)��(sh��)��
����ȡ��һ��(g��)��(sh��)��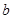 �Ǐą^(q��)�g
�Ǐą^(q��)�g ����ȡ��һ��(g��)��(sh��)����
����ȡ��һ��(g��)��(sh��)���� �](m��i)�Ќ�(sh��)���ĸ��ʣ�
�](m��i)�Ќ�(sh��)���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com