
已知函數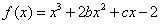 的圖象在與
的圖象在與 軸交點處的切線方程是
軸交點處的切線方程是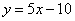 .
.
(Ⅰ)求函數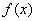 的解析式;
的解析式;
(Ⅱ)設函數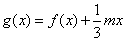 ,若
,若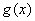 的極值存在,求實數
的極值存在,求實數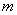 的取值范圍以及當
的取值范圍以及當 取何值時函數
取何值時函數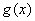 分別取得極大和極小值.
分別取得極大和極小值.
(1)
(2)當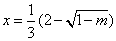 時
時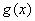 有極大值;
有極大值;
當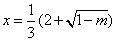 時
時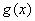 有極小值
有極小值
【解析】
試題分析:解:(1)由已知,切點為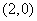 ,故有
,故有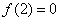 ,
,
即 ①
1分
①
1分
又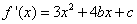 ,由已知,
,由已知, 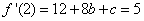 .
.
得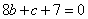 ② 3分
② 3分
聯立①②,解得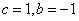 ,
,
于是函數解析式為 5分
5分
(2) 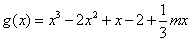 ,
,
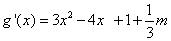 ,令
,令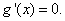 6分
6分
當函數有極值時,方程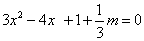 必有實根,
必有實根,
由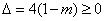 ,得
,得 . 8分
. 8分
①當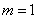 時,
時, 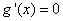 有實根
有實根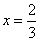 ,在
,在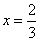 左右兩側均有
左右兩側均有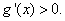 ,故函數
,故函數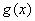 無極值.
無極值.
②當 時,
時, 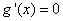 有兩個實根,
有兩個實根, 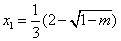 ,
, 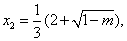
當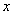 變化時,
變化時, 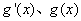 的變化情況如下表:
的變化情況如下表:
|
x |
(-∞,x1) |
x1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
g′(x) |
+ |
0 |
- |
0 |
+ |
|
g(x) |
↗ |
極大值 |
↘ |
極小值 |
↗ |
11分
故當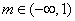 時,函數
時,函數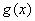 有極值:當
有極值:當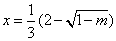 時
時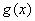 有極大值;
有極大值;
當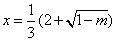 時
時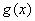 有極小值. 12分
有極小值. 12分
考點:導數的運用
點評:主要是考查了導數在研究函數中的運用,屬于基礎題。


科目:高中數學 來源: 題型:
已知函數![]() 的圖象在與
的圖象在與![]() 軸交點處的切線方程是
軸交點處的切線方程是![]() 。
。
(I)求函數![]() 的解析式;
的解析式;
(II)設函數![]() ,若
,若![]() 的極值存在,求實數
的極值存在,求實數![]() 的取值范圍以及函數
的取值范圍以及函數![]() 取得極值時對應的自變量
取得極值時對應的自變量![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分)
已知函數![]() 的圖象在與
的圖象在與![]() 軸交點處的切線方程是
軸交點處的切線方程是![]() 。
。
(1)求函數![]() 的解析式;
的解析式;
(2)設函數![]() ,若
,若![]() 的極值存在,求實數
的極值存在,求實數![]() 的取值范圍以及函數
的取值范圍以及函數![]() 取得極值時對應的自變量
取得極值時對應的自變量![]() 的值。
的值。
查看答案和解析>>
科目:高中數學 來源:2010屆高三數學每周精析精練:函數 題型:解答題
已知函數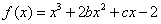 的圖象在與
的圖象在與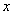 軸交點處的切線方程是
軸交點處的切線方程是 。
。
(I)求函數 的解析式;
的解析式;
(II)設函數 ,若
,若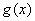 的極值存在,求實數
的極值存在,求實數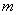 的取值范圍以及函數
的取值范圍以及函數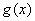 取得極值時對應的自變量
取得極值時對應的自變量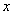 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com