
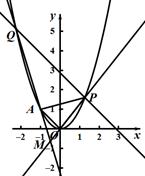
(本小題滿分1 2分)在平面直角坐標(biāo)系xOy中,已知點(diǎn)A(一1,1),P是動(dòng)點(diǎn),且三角形POA的三邊所在直線的斜率滿足kOP+kOA=kPA.
(I)求點(diǎn)P的軌跡C的方程;
(Ⅱ)若Q是軌跡C上異于點(diǎn)P的一個(gè)點(diǎn),且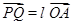 ,直線OP與QA交于點(diǎn)M,試探究:點(diǎn)M的橫坐標(biāo)是否為定值?并說明理由.
,直線OP與QA交于點(diǎn)M,試探究:點(diǎn)M的橫坐標(biāo)是否為定值?并說明理由.
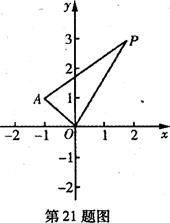
解:(Ⅰ)設(shè)點(diǎn)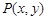 為所求軌跡上的任意一點(diǎn),則由
為所求軌跡上的任意一點(diǎn),則由 得
得
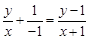 ,·························· 2分
,·························· 2分
整理得軌跡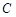 的方程為
的方程為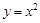 (
(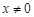 且
且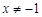 ),…4分
),…4分
(Ⅱ)(方法一)設(shè)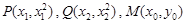 ,
,
由 可知直線
可知直線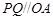 ,則
,則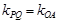 ,
,
故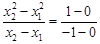 ,即
,即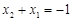 ,…………………6分
,…………………6分
由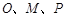 三點(diǎn)共線可知,
三點(diǎn)共線可知, 與
與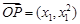 共線,
共線,
∴ 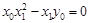 ,
,
由(Ⅰ)知 ,故
,故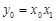 ,··················· 8分
,··················· 8分
同理,由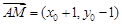 與
與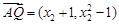 共線,
共線,
∴ 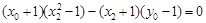 ,即
,即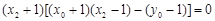 ,
,
由(Ⅰ)知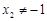 ,故
,故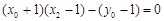 ,·········· 10分
,·········· 10分
將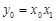 ,
,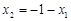 代入上式得
代入上式得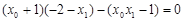 ,
,
整理得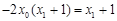 ,
,
由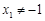 得
得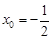 ,即點(diǎn)M的橫坐標(biāo)為定值
,即點(diǎn)M的橫坐標(biāo)為定值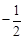 .·········· 12分
.·········· 12分
(方法二)
設(shè)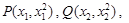
由 可知直線
可知直線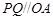 ,則
,則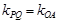 ,
,
故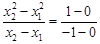 ,即
,即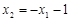 ,················· 6分
,················· 6分
∴直線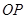 方程為:
方程為: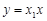 ①;·················· 8分
①;·················· 8分
直線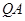 的斜率為:
的斜率為: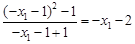 ,
,
∴直線 方程為:
方程為: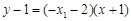 ,即
,即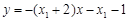 ②;· 10分
②;· 10分
聯(lián)立①②,得 ,∴點(diǎn)
,∴點(diǎn) 的橫坐標(biāo)為定值
的橫坐標(biāo)為定值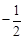 .·········· 12分
.·········· 12分
【解析】略


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年山東省濰坊市高三3月第一次模擬考試文科數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿分1 2分)
如圖,四邊形ABCD中,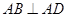 ,AD∥BC,AD =6,BC =4,AB =2,點(diǎn)E、F分別在BC、AD上,EF∥AB.現(xiàn)將四邊形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,點(diǎn)E、F分別在BC、AD上,EF∥AB.現(xiàn)將四邊形ABEF沿EF折起,使平面ABCD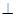 平面EFDC,設(shè)AD中點(diǎn)為P.
平面EFDC,設(shè)AD中點(diǎn)為P.
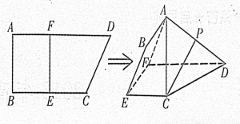
( I )當(dāng)E為BC中點(diǎn)時(shí),求證:CP//平面ABEF
(Ⅱ)設(shè)BE=x,問當(dāng)x為何值時(shí),三棱錐A-CDF的體積有最大值?并求出這個(gè)最大值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年福建省福州市高三第一學(xué)期期末質(zhì)量檢測(cè)文科數(shù)學(xué) 題型:解答題
.(本小題滿分1 2分)設(shè)△ABC的內(nèi)角A、B、C所對(duì)的邊分別為a、b、c.已知a=3,B=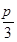 ,S△ABC=6
,S△ABC=6
( I )求△ABC的周長(zhǎng);
(Ⅱ)求sin2A的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分1 2分)
在直三棱柱![]() 中,
中,![]() ,
,![]() ,且異面直線
,且異面直線![]() 與
與![]() 所成的角等于
所成的角等于![]() ,設(shè)
,設(shè)![]() .
.
 (Ⅰ)求
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成的銳二面角的大小.
所成的銳二面角的大小.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com